The following is some equations and functions that are essential to Physics 1110. They are taken directly from the following Physics book:
If we know the magnitude A of a vector A and its direction,
given by an angle 
, we can calculate the components.
and 
We define the vector product to be a vector quantity with a
direction perpendicular to a plane in which two vectors lie and with a
magnitude of 
.
In other words, the vector product 
The average velocity is a vector in a certain
direction with an x -component as follows:
where 
is
the velocity at the initial time t = 0.
where 
is the initial velocity and 
is
the initial position. Acceleration is constant.
where is the
change in position. The components of this vector are
as follows:
where the components of this vector are as follows:
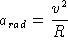where R
is the radius of the circle and the acceleration points
inward towards the center of the circle.
where 
is the
acceleration due to gravity.
or 
A particle is in equilibrium if 
.
where
is the
sliding friction, 
is the normal force, and 
is the
coefficient of kinetic friction.
where
is the static friction force, 
is the coefficient
of static friction, and is the normal force.
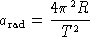where R is the radius and T is the period and is equal
to 
.
(pgs. 164-181 Sections 6-2 to 6-4)
where 
and 
are displacements, F is the magnitude of the
applied force, and W is work.
where 
and 
are
points along a curve, 
are initesimal vector
displacements, and 
is the angle between 
and
(pg. 155)
(pg. 159)
(pg. 160)
where U is the
gravitational potential energy, mg is the weight of the
object, and y is the displacement.
where U is
the elastic potential energy, k is the force constant of
the spring, and x is the extension displacement.
where 
is the
momentum, m is the mass, and 
is the velocity
vector.
The following is a restatement of Newton's Second Law:
where 
is momentume, is the force, and
is the momentum. (pg. 210)
(pg. 211)
where I is the moment of
inertia, 
.
where is the force and 
is the position vector that is
perpendicular to that force.
where 
is the total torque of the couple about an arbitrary
point o, F is the is the magnitude of each force, and l is the
perpendicular distance separating the two forces.
For the following, r is displacement, is the angle in
radians, 
is angular velocity, and 
is the angular
acceleration. Any 
is that variable at time zero.
Average angular velocity is as follows:
Instantaneous angular velocity is as follows:
Average angular velocity is as follows:
Instantaneous angular velocity is as follows:
Another way to express angular acceleration:
acceleration, is angular velocity, r is
where I is the momoent of inertia and
is equal to 
where m is the mass of the particle and
r is its distance from the center of rotation.
where dm are small mass elements of a body, r is the distance from the
axis of rotation, 
is the density of the body.
where
is the center-of-mass velocity and 
is the momoent of
inertis for an axis trhought tha center of mass ( 
) where M is mass and R is radius.
The following relationships are fully derived in the text. See the referenced pages.
All of the variables have been previously defined.
where 
is the angular momentum,
is the position vector, is the momentum, 
is torque, I is the
moment of inertia, amd is the angular velocity.