![]()
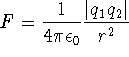 where F is the force of interaction;
where F is the force of interaction; ![]() ;
; ![]() and
and ![]() are point charges; and
r is the distance between the two point charges.
are point charges; and
r is the distance between the two point charges.
![]()
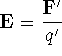 where
where ;
q' is the test charge;
![]() is the electrical force; and
is the electrical force; and
![]() is the electrical field. The direction of the
electrical field and force are the same.
is the electrical field. The direction of the
electrical field and force are the same.
![]()
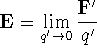
![]()
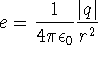
![]()
![]() where p is the
electric
dipole moment, E is the electric field, and
where p is the
electric
dipole moment, E is the electric field, and ![]() is the
angle between the vectors
is the
angle between the vectors ![]() and
and ![]() .
.
![]() Another way to write this equation is as
a cross product:
Another way to write this equation is as
a cross product: ![]()
![]()
where ![]() is the electric field vector; dA is the slice of
area that
is the electric field vector; dA is the slice of
area that ![]() is going through; and
is going through; and ![]() is the angle
between the perpendicular and dA. Therefore
is the angle
between the perpendicular and dA. Therefore ![]() is the surface area through which
is the surface area through which ![]() flows.
flows.
![]() Another way to express the electric flux is as
follows:
Another way to express the electric flux is as
follows: ![]() where q is
a point charge and
where q is
a point charge and ![]() is a universal constant. This
eqation only applies to the electric flux in a sphere. (pg. 640
Section 23-2)
is a universal constant. This
eqation only applies to the electric flux in a sphere. (pg. 640
Section 23-2)
![]()
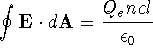 where
where ![]() is the total charge enclosed
by the
surface. Thus this integral must always be over a closed
surface.
is the total charge enclosed
by the
surface. Thus this integral must always be over a closed
surface.
![]()
![]() where
where ![]() is the surface charge density of the plates and the plates are
oppositely charged.
is the surface charge density of the plates and the plates are
oppositely charged.
![]()
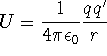 where U is the electric potential energy; and q' is a
test charge a distance r from the charge q.
where U is the electric potential energy; and q' is a
test charge a distance r from the charge q.
![]() When there are many test charges, the electric
potential energy can be expressed as follows:
When there are many test charges, the electric
potential energy can be expressed as follows: 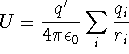 .
.
![]()
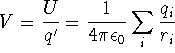 where V is the potential.
where V is the potential.
![]()
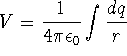
![]()
![]() where
where ![]() is the potential difference and equals the
work done by an external force.
is the potential difference and equals the
work done by an external force.
![]()
![]() The expression is read as
"
The expression is read as
" ![]() is the negative of the gradient of V." This can also be
expressed as components:
is the negative of the gradient of V." This can also be
expressed as components:
![]()
![]()
![]()
![]()
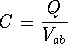 where C is capacitance
and is measured in Farads and
where C is capacitance
and is measured in Farads and ![]() is the potential
difference between the conductors.
is the potential
difference between the conductors.
![]()
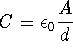 where A is the
area of the capacitor and d is the distance between the
capacitors.
where A is the
area of the capacitor and d is the distance between the
capacitors.
![]()
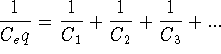 This equation is for capacitors that
are in series.
This equation is for capacitors that
are in series.
![]()
![]() This
equation is
for capacitors that are in parallel.
This
equation is
for capacitors that are in parallel.
![]() To calculate the potential energy U of a charged
capacitor, one can calculate the work required to charge
it.
To calculate the potential energy U of a charged
capacitor, one can calculate the work required to charge
it.
![]()
Thus, defining the potential energy of an uncharged capcaitor as zero:
![]()
![]()
![]() where I is the current which
is the net charge flow dQ through an area in the time dt.
where I is the current which
is the net charge flow dQ through an area in the time dt.
![]()
![]() where J is the current
density; A is the cross-section area; n is the
concentration of particles; and
where J is the current
density; A is the cross-section area; n is the
concentration of particles; and ![]() is the magnitude of the
drift velocity.
is the magnitude of the
drift velocity.
![]()
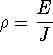 where
where ![]() is
resistivity, J is
the current density, and E is the electric field.
is
resistivity, J is
the current density, and E is the electric field.
![]()
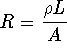 where
where ![]() is
resistivity; L
is the length of the conductor; and A is the cross-sectional
area of the conductor.
is
resistivity; L
is the length of the conductor; and A is the cross-sectional
area of the conductor.
![]()
![]()
![]()
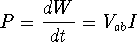
![]()
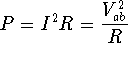
![]()
![]() (resistors in
series)
(resistors in
series)
![]()
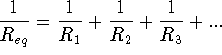 (resistors in parallel)
(resistors in parallel)
![]() The following is the Junction Rule:
The following is the Junction Rule: ![]() (any
junction)
(any
junction)
![]() The following is the Loop Rule:
The following is the Loop Rule: ![]() (any
closed loop)
(any
closed loop)
![]()
![]() The force on a charge
The force on a charge
![]() moving with velocity
moving with velocity ![]() in a magnetic field
in a magnetic field ![]() .
.
![]()
![]()
![]()
![]() where
where ![]() are
infitesimal segments of a conductor and
are
infitesimal segments of a conductor and ![]() is the force on
each segment in the magnetic field,
is the force on
each segment in the magnetic field, ![]() .
.
![]()
![]() where A is the area of
the loop, I is the current flowing through it, and
where A is the area of
the loop, I is the current flowing through it, and ![]() is the
angle the loop is from the perpendicular.
is the
angle the loop is from the perpendicular.
![]()
![]() where
where ![]() is the
magnetic
moment and is equal to IA.
is the
magnetic
moment and is equal to IA.
![]()
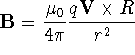 where R is a unit vector equal to
where R is a unit vector equal to ![]() ,
r being
the distance from the charge. Also,
,
r being
the distance from the charge. Also, ![]() is the perticle's
velocity.
is the perticle's
velocity.
![]()
![]()
![]()
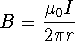 where r is the
radial distance of the magnetic field away from the center of the
conductor.
where r is the
radial distance of the magnetic field away from the center of the
conductor.
![]()
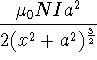 where N is the number of circular loops a is the radius of the
circular conductor, and x is the distance to a point.
where N is the number of circular loops a is the radius of the
circular conductor, and x is the distance to a point.
![]()
![]() where
where
![]() is the algebraic sum of the currents enclosed or linked
by the integration path.
is the algebraic sum of the currents enclosed or linked
by the integration path.
![]() The angular velocity of the perticle is as follows:
The angular velocity of the perticle is as follows:
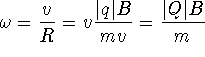 where
R is the radius of the circular path.
where
R is the radius of the circular path.
![]()
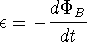 Thus, the induced
emf in a circuit equals the negative of the time rate of
change of
magnetic flux through the circuit.
Thus, the induced
emf in a circuit equals the negative of the time rate of
change of
magnetic flux through the circuit.
![]()
![]() where L is the length of a given
rod.
where L is the length of a given
rod.
![]() For any two points a and b the motional emf in the
direction from b to a is
For any two points a and b the motional emf in the
direction from b to a is ![]() q
q