Building Bridges in the First Two Years

Project #2: Not-so-simple Harmonic Oscillator

Simple harmonic motion is a fundamental model for sound, mechanical vibrations, and traveling waves in physics and engineering. The purpose of this project is to use calculus and Maple to explore and illustrate some of the basic properties of the equations involved. Here are some questions to move you along.

1. The function 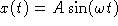, for constants A and , can be used to describe the motion of a mass attached to a spring.
   1. Choose values for A and and plot position and velocity on the same set of axes. Is it true that velocity is zero when position is maximized? Is it true that velocity is maximized when position is zero?
   2. Graph the square of position and the square of velocity on the same axes. Find constants and 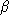so that the graph of

      

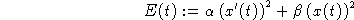
      is equal to a constant. Compute the derivative to verify that your constants work.

   3. Look up kinetic and potential energy in your physics text. Use these ideas to explain the results from part (b).

2. Define 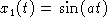and 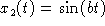for some constants a and b. We want to study the effect of changing a and b on the function .
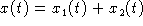   1. Choose values for a and b to obtain interesting plots of the graphs of 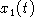, , 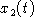and 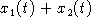(separately or on the same set of axes).

      Be sure to explore a range of b values for each fixed a. (Be sure also to explore a sufficiently large t-interval in your plots.) Carefully describe what you see regarding the amplitude and frequencies that you observe. (For fun, you can use the animate command to get nice movies of the phenomenon as a or b vary.)

      The phenomena that you have (or should have) observed in the mathematics are called beats. You might want to look this up in your physics text.

   2. There is an obvious ``envelope'' that appears in your plots. Try to use some basic trigonometric identities to find an equation for this envelope and determine its amplitude.
   3. Find the largest interval containing t=0 on which the sum 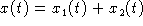is increasing. It is hard to get an exact solution, so explain your method clearly, and indicate its accuracy.

      
      

      Back to the Bridge Projects Home Page Last modified: Mon Jul 28 12:39:57 EDT 1997