Background

Maple has several useful commands for working with vectors and vector-valued functions. This lab will introduce you to five different commands for working with vectors. Later on in the course, we will learn more commands, including commands for dealing with vector-valued functions.

The commands in this lab are all in the Maple linalg package, which must be loaded first with the following command.

  > with(linalg):

Warning: new definition for   norm
Warning: new definition for   trace

Here is a list of the Maple functions we will be using from this package. Note that these functions form only a small subset of the package, which is designed primarily for linear algebra. Examples are given below, more examples can be found in the help screens for each command. In the list, vector can refer to either a vector or a vector-valued function.

vector

Used to define a vector.

add

Adds two vector together.

scalarmul

Multiplies a vector by a scalar.

dotprod

Computes the dot product of two vectors.

evalm

Evaluates expressions involving vectors.

The examples below show how to use the vector function to define two and three-dimensional vectors, and how to use the add, scalarmul, and dotprod commands. Note that you cannot mix vectors with different dimensions.

  > a := vector([1,1,1]);

  > b := vector([2,0,3]);

  > c := vector([0,-1,-3]);

  > d := vector([1,2]);

  > e := vector([1,-1]);

  > add(a,e);

Error, (in add) vector dimensions incompatible

  > dotprod(d,e);

  > add(a,b);

  > add(a,add(b,c));

  > scalarmul(a,5);

  > dotprod(a,b);

  > dotprod(a,c);

If you are adding several vectors together, using the add and scalarmul commands can get very tedious. An alternative is to use the evalm command, which allows you to use standard mathematical syntax, as shown in the following example. Unfortunately, there is not a standard notation for the dot product, so you still have to use the dotprod command.

  > evalm(2*a-b);

In the examples above, we worked with fixed vectors, that is, we worked with vectors whose components were fixed numbers. It is also possible, however, to define and manipulate vectors whose components are not fixed. Examples are given below.

  > u := vector(3);

  > v := vector(3);

  > add(u,v);

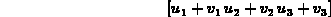
  > scalarmul(u,2);

  > dotprod(u,u);

  > dotprod(u,v);

  > dotprod(v,u);

  > evalm(u-v);

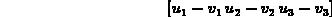
  > evalm(2*v);