Background

Maple has several useful commands for working with vectors and vector-valued functions. This lab will make use of about twelve of these commands. About half are in the linalg package, and the other half are in the CalcP package of functions written at WPI. Before you can use these commands, you must load them, using the with command.

Maple functions from the linalg package

Here is a list of the Maple functions we will be using from this package. Note that these functions form only a small subset of the package, which is designed primarily for linear algebra. Examples for some of the commands are given below, more examples can be found in the help screens for each command.

vector

Used to define a vector or vector-valued function.

add

Adds two vectors or vector-valued functions together.

scalarmul

Multiplies a vector or a vector-valued function by a scalar.

dotprod

Computes the dot product of two vectors or vector-valued functions.

crossprod

Computes the cross product of two vectorsor vector-valued functions.

evalm

Evaluates expressions involving vectors or vector-valued functions.

Examples

  > with(linalg):

Warning: new definition for   norm
Warning: new definition for   trace

  > with(CalcP):

  > u := vector([1,2,3]);

  > f := t-> vector([t,t^2,t^3]);

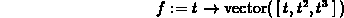
  > g := t -> vector([cos(t),sin(t),t]);

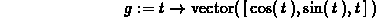
  > h := t -> vector([cos(t),sin(2*t)]);

To add vectors, or multiply them by scalars, you can use the Maple add and scalarmul commands, or use standard math notation and use the evalm command.

  > add(u,g(t));

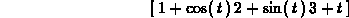
  > evalm(t^4*u+2*f(t)-g(t));

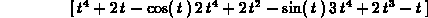
  > scalarmul(u,t^2);

The individual components of a vector are also available in Maple, as shown below. You can use this to extract the individual functions for plotting or further manipulation.

  > u[3];

  > f(t)[1];

  > g(t)[2];

The linalg package has procedures for the dot product and the cross product. The latter procedure, however, works only on vectors with three components and the former procedure requires two vectors with the same number of components, so beware. Some examples are shown below.

  > dotprod(u,f(t));

  > crossprod(u,g(t));

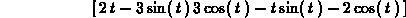
  > crossprod(f(t),g(t));

Maple functions from the CalcP package.

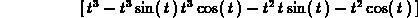
These functions are all specifically written for use in calculus. The list below gives the names of the procedures we will be using, as well as brief descriptions. Maple help screens are available for all of these functions, so refer to them for further examples.

VDiff

Differentiates vector-valued functions.

VPlot

Plots vector-valued functions in two and three dimensions.

VMag

Computes the magnitude of a vector.

ParamPlot

Animates parametric curves in two dimensions.

ParamPlot3D

Animates parametric curves in three dimensions.

Speed

Computes the speed of a particle moving on a path defined by a vector-valued function .

Examples

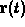For more examples, see the help screens. You have already seen the ParamPlot function, ParamPlot3D works in a very similar fashion. Both ParamPlot and ParamPlot3D will take a vector or a list of functions as their first argument. Don't forget to load the CalcP package if you have not already done so.

  > VDiff(g(t),t);

  > VDiff(g(t),t,t);

  > VPlot(f(t),t=-2..2);

  > VPlot(g(t),t=0..4*Pi);

  > VPlot(h(t),t=0..2*Pi);

  > ParamPlot(h(t),t=0..2*Pi);

  > ParamPlot3D(g(t),t=0..4*Pi);

  > VMag(h(t));

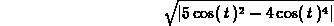
The Speed function can either give the speed at a fixed value of t, or give the speed as a vector expression involving t. See the examples below.

  > Speed(f(t),t=1);

  > Speed(f(t),t);

  > Speed(g(t),t);