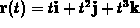Exercises

1. For the example with 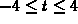, answer the following questions.
   1. For which value(s) of t is the speed a maximum?
   2. For which value(s) of t is the speed a minimum?
   3. For which value(s) of t is the curvature a maximum?
   4. For which value(s) of t is the curvature a minumum?

2. Consider the curve .
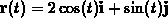   1. Show that the image curve of 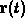is an ellipse. That is, find values of a and b such that the component functions of 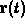satisfy the equation

      

   2. Find the values of t, 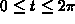, for which the curvature of 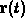is a maximum or a minimum and identify which is which.
   3. Find the values of t, 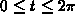, for which the speed for the trajectory 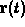is a maximum or a minimum and identify which is which.

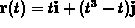3. Consider . What is the normal vector 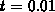at ? At 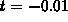? What about at t=0? What goes wrong?

4. Consider the helix

   

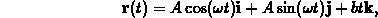
   where A, b, and are parameters.

   1. Plot 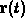for a few values of the parameters. Try to identify how each parameter affects the curve. A good way to do this is with the subs command, like the following example.

        > VPlot(subs({A=1,b=1,omega=1},r(t)),t=0..2*Pi);
      

   2. Show, using the Speed command that the speed is constant and describe how it depends on the parameters.
   3. Compute the curvature and describe how it depends on the parameters.