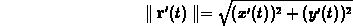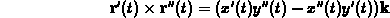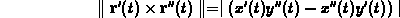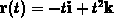MA 1004 D-95 Sample Exam 1

Show your work in the space provided. Unsupported answers may not receive full credit. Use the backs of the pages if needed. (In the real exam, there will be plenty of space for your work.)

1. Sketch a graph of the image curve of the vector-valued function for 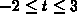. On your sketch, clearly identify the points corresponding to t = -1 and t=2.

   Answer: See the sketch on the bulletin board opposite SH 105A.

2. Suppose a position function for a particle is given by .
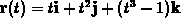   1. Compute the velocity of the particle.

      Answer:

      

   2. Compute the speed of the particle.

      Answer:

      

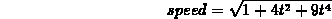
   3. Compute the acceleration of the particle.

      Answer:

      

   4. Find all values of t for which the velocity is perpendicular to the acceleration.

      Answer:

      

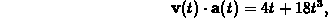
      so the only value of t where 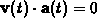is t=0

3. Determine whether the following equation is generally true.

   

   Hint - if you can find a simple vector valued function for which the equation is not true, then the equation is not true in general.

   Answer:
   Try .

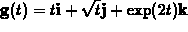4. If , compute the following definite integral.

   

   Answer:

   

5. Set up, but do not evaluate, an integral giving total distance traveled (i.e.the arc-length) between t=0 and t=10 for the position function .

   Answer:

   

6. Compute the unit tangent vector corresponding to the position function

   

   Answer:

   

7. Compute the curvature of

   

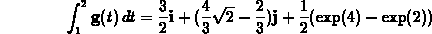
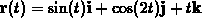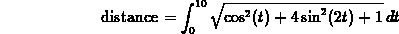
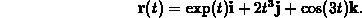
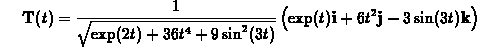
   Answer:

   

   

   

   So

   

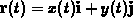8. If is a two-dimensional vector valued function with component functions 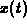and 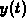, show the the curvature is given by

   

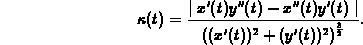
   Answer:

   

   

   

   

   

• About this document ...