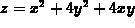 . You may restrict your attention to the rectangle
. You may restrict your attention to the rectangle 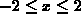 and
and 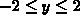 .
.
Answer: (partial)
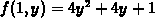 and
and 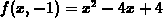 .
.
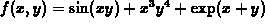 .
.
Answer:
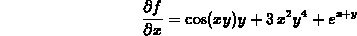
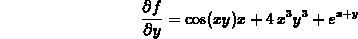
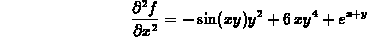
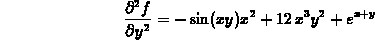
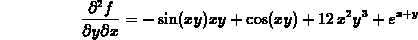
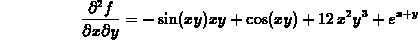
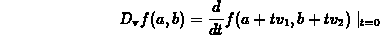
to compute the directional derivative of the function 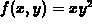 at the point
at the point 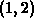 in the direction of the vector
in the direction of the vector 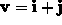 .
.
Answer:
a = 1, b=2, and the unit vector in the direction of 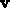 is
is
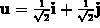 so we
have
so we
have
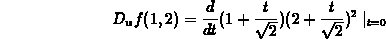
or
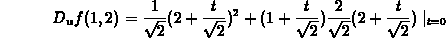
So
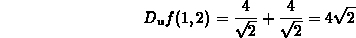
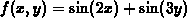 at the
point x=0, y=0.
at the
point x=0, y=0.
Answer:

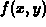 at a particular point
at a particular point
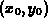 is perpendicular to the level curve through this same
point.
is perpendicular to the level curve through this same
point.
Answer:
Suppose that 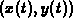 is a parametrization of the contour that
passes through the point
is a parametrization of the contour that
passes through the point 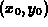 at t=0. Then
at t=0. Then

for some constant C. Differentiating both sides of this equation, using the chain rule, and writing the result as a dot product gives
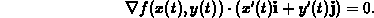
Evaluating this at t=0 gives
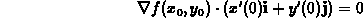
and recognizing that the vector 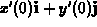 is tangent to the contour at the point in question
gives the result.
is tangent to the contour at the point in question
gives the result.
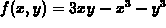 .
.
Answer:
Critical points are where the gradient of f vanishes, or the
solutions of the equations

Eliminating x gives the single equation 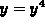 . Solving this
equation and computing the corresponding values of x gives the two
solutions x=0, y=0, and x=1, y=1.
. Solving this
equation and computing the corresponding values of x gives the two
solutions x=0, y=0, and x=1, y=1.
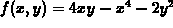 on the square domain
on the square domain 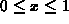 ,
, 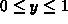 .
.
Answer:
The first step is to find the critical points.
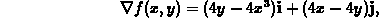
so x=y and 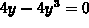 at the critical points. So the critical
points are x=0, y=0, and x=1, y=1.
at the critical points. So the critical
points are x=0, y=0, and x=1, y=1.
The second step is to analyze 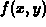 on the boundaries.
on the boundaries.
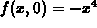 , which has a critical point a x=0.
, which has a critical point a x=0.
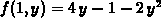 , which has a critical point at y=1.
, which has a critical point at y=1.
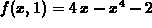 , which has a critical point at x=1.
, which has a critical point at x=1.
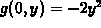 , which has a critical point at y=0.
, which has a critical point at y=0.
In the third step, we evaluate f at all the candidate points. Here
the candidates are the four corner points 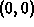 ,
, 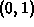 ,
,
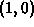 , and
, and 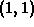 . We have
. We have
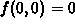 ,
, 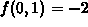 ,
, 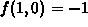 and
and 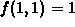 so the
minimum is -2 at
so the
minimum is -2 at 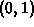 and the
maximum is 1 at
and the
maximum is 1 at 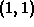 .
.
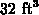 is to be
constructed out of material that costs
is to be
constructed out of material that costs 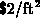 for the sides
and
for the sides
and 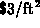 for the top and bottom. Write down the cost
function for this box as a
function of the three dimensions x, y, and z of the box. Using
the method of Lagrange multipliers, set
up, but do not solve, the equations for determining the box dimensions
that would minimize the cost.
for the top and bottom. Write down the cost
function for this box as a
function of the three dimensions x, y, and z of the box. Using
the method of Lagrange multipliers, set
up, but do not solve, the equations for determining the box dimensions
that would minimize the cost.
Answer:
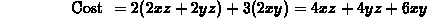
and the constraint is xyz=32, so the function to be minimized is
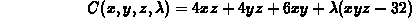
so the equations to be solved to minimize the cost are
