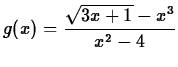The connection is that expressions are often used to define
functions. That is, we could let
![]() , which defines a
function
, which defines a
function ![]() . The rule for this function is to substitute a value for
. The rule for this function is to substitute a value for
![]() into the expression
into the expression ![]() to obtain the output value. Not
all expressions can be used to define functions, however, and not all
functions are defined by expressions so these really are distinct
mathematical objects.
to obtain the output value. Not
all expressions can be used to define functions, however, and not all
functions are defined by expressions so these really are distinct
mathematical objects.
Maple mimics this mathematical distinction between expression and function. You can define expressions in Maple and even label them for later use with commands like the one below.
> p := x^2+sin(3*x);This is an expression not a function, which means there is no rule associated with it. Thus evaluating the expression at a specific value of
> subs(x=2,p);The syntax for defining a function in Maple uses an arrow to make the idea of a function as a process explicit. For example, we can define a function
> f := x -> x^2+sin(3*x);Evaluating our function at a specific value of
> f(2);One final thing to note is that Maple will use f to denote the function we have defined, but will use f(x) to denote the expression used to define the function.
> F(x) := x^2+3;Since Maple doesn't complain, students often think that what they've done is correct. The output from the following commands, however, shows that the object we've defined doesn't behave like a function.
> F(x); > F(1); > F(t); > F(2*x);What is happening here is that we've defined something called a table in Maple. For the input
When you use the D operator to compute the derivative of a function, the result is also a function, as shown below.
> D(f);If you provide a label, then you get a function you can use later in the session,
> df := D(f);However, this is usually not necessary. See the examples below.
If you want to evaluate the derivative at a specific value of ![]() or
just get the expression for the derivative, you can use the following
forms of the D operator.
or
just get the expression for the derivative, you can use the following
forms of the D operator.
> D(f)(2); > D(f)(x);This last form is the one to use for plotting, as shown below.
> plot(D(f)(x),x=-2..2);
The D operator cannot be used on expressions, for example trying to use it to differentiate the expresssion we defined above results in an error.
> D(p);If you recall that Maple uses f(x) to refer to the expresssion that is used to define
> D(f(x));
To differentiate expressions, you need to use the diff command. Here is an example.
> diff(p,x);The diff command can also be applied to functions as shown below.
> diff(f(x),x);Note, however, that the result of the diff command is an expression, not a function. This means that computing the value of the derivative at a specific value of