


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to introduce you to the basics needed in any Maple lab. The main topics include: assigning labels, defining expressions, defining functions and plotting.
Expressions such as 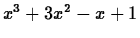 can be entered in a similar way to variable assignment. Choose a variable name to represent the expression and assign the expression to the variable as follows.
can be entered in a similar way to variable assignment. Choose a variable name to represent the expression and assign the expression to the variable as follows.
> expr := x^3+3*x^2-x+1;
Note that in the expression above, there is an asterisk between 3 and 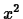 . A common mistake is to write two functions next to each other without the "*" symbol. This would give incorrect results when using this expression since Maple doesn't understand implied multiplication.
Suppose you want to enter the same expression stored in expr above, but as a function of
. A common mistake is to write two functions next to each other without the "*" symbol. This would give incorrect results when using this expression since Maple doesn't understand implied multiplication.
Suppose you want to enter the same expression stored in expr above, but as a function of 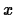 . In Maple, you would type
. In Maple, you would type
> f := x-> x^3+3*x^2-x+1;
Below is how NOT to enter a function:
> f(x) := x^3+3*x^2-x+1;
The difference between expressions and functions are first the obvious, that expressions do not have to satisfy the definition of a function in the sense that for each input 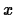 , there is a unique value
, there is a unique value 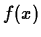 . A function may be defined as an expression, but not all expressions can be defined as functions. The differences in Maple are numerous as you will see below when we evaluate the expression or function for a given value as well as when using the plot command.
In order to evaluate an expression at a given value of
. A function may be defined as an expression, but not all expressions can be defined as functions. The differences in Maple are numerous as you will see below when we evaluate the expression or function for a given value as well as when using the plot command.
In order to evaluate an expression at a given value of 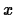 , you must use the subs command. For example, if we wanted to evaluate the expression expr
, you must use the subs command. For example, if we wanted to evaluate the expression expr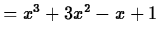 at
at 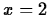 , the example below show how this can be done
, the example below show how this can be done
> subs(x=2,expr);
> r:=sin(theta) + 8*theta^2;
> subs(theta=1/2*Pi,r);
In the subs command, the first argument tells Maple what you would like to substitute in for 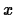 . The second argument tells Maple what expression you are substituting into. Note the difference in outputs when a whole number or fraction is entered compared to a decimal.
. The second argument tells Maple what expression you are substituting into. Note the difference in outputs when a whole number or fraction is entered compared to a decimal.
>g:=2*x/3;
>subs(x=4,g);
>subs(x=4.0,g);
In Maple, functions are much easier to evaluate than expressions. In order to evaluate the function
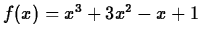 at
at 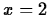 , simply type
, simply type
> f(2);
Here are a few more examples of evaluating functions.
> f(a+h);
> f(Pi);
> evalf(f(Pi));
Note the use of the evalf command in the last example above. This command is used when we want Maple to output the answer in decimal form. If this command is not used, the output to your Maple commands will be calculated analytically, where as the evalf command forces Maple to calculate the answers numerically. The evalf command has one essential argument, however a second argument can be added in order to tell how many digits we want to be in the answer. The example below evaluates 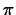 using 10 digits, not 10 decimal places.
using 10 digits, not 10 decimal places.
> evalf(Pi,10);
The following example shows how the Maple plot command is used to plot the previously entered function 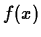 and expressions
and expressions 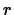 .
.
> plot(f(x),x=-5..2);
> plot(r,theta=-2*Pi..2*Pi);
The plot command above has two essential arguments. The first argument is the function(s) or expression(s) that you want to plot. The function or expression can be typed in before the plot command or you can simply type it in as the first argument. The second argument is the range of numbers for the 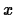 -axis. The plot command allows you to add additional optional arguments as well. For instance, you may want to also restrict the y-axis range or add a title to your plot.
-axis. The plot command allows you to add additional optional arguments as well. For instance, you may want to also restrict the y-axis range or add a title to your plot.
> plot(x^2,x=-2..2,y=-5..5,title=''My First Plot'');
This particular command allows you to add arguments, but if you were to leave off one of the essential arguments, you will get an error message. You can also plot more than one function or expression on the same graph by enclosing them in square brackets [ ] and separating them by commas. For example, we can plot 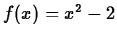 and
and 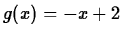 on the same graph.
on the same graph.
> f := x-> x^2-2;
> g := x-> -x+2;
> plot([f(x),g(x)],x=-4..4,color=[``DarkOrchid'',''Gold'']);
>?plot,colornames
- Enter
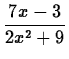 as an expression.
as an expression.
- A)
- Evaluate this expression at
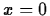 .
.
- B)
- Evaluate this expression at
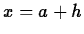 .
.
- C)
- Evaluate this expression at
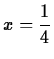 .
.
- D)
- Evaluate this expression at
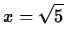 and make sure your output is in decimal form.
and make sure your output is in decimal form.
- E)
- Plot this expression over the
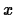 range
range
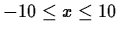 .
.
- Repeat all parts of exercise 1 by first defining
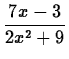 as a function.
as a function.
- Define
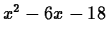 and
and 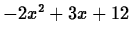 as functions. Plot them both on the same graph. Estimate the two intersection points by observing the plot. Plug each
as functions. Plot them both on the same graph. Estimate the two intersection points by observing the plot. Plug each 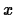 value back into both functions to show that the
value back into both functions to show that the 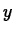 values are the same.
values are the same.



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2011-08-17
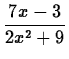 as an expression.
as an expression.
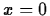 .
.
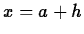 .
.
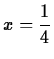 .
.
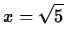 and make sure your output is in decimal form.
and make sure your output is in decimal form.
 range
range
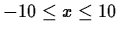 .
.
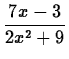 as a function.
as a function.