


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The limit definition of the derivative of 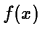 often written as
often written as 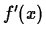 is defined as:
is defined as:
It can be interpreted geometrically as the slope of the tangent line to the graph of 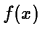 at a point
at a point 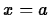 and functionally as the instantaneous rate of change of
and functionally as the instantaneous rate of change of 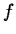 at
at 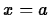 .
You can use the definition and the Maple limit command to compute derivatives directly, as shown below. You can also compute derivatives using Maple's diff or D command.
The following limit determines f'(x).
.
You can use the definition and the Maple limit command to compute derivatives directly, as shown below. You can also compute derivatives using Maple's diff or D command.
The following limit determines f'(x).
> limit((f(x+h)-f(x))/h,h=0);
The example below shows how to use the limit definition of derivative to find 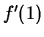 with Maple.
with Maple.
> f := x -> x^2+3*x+5;
> limit((f(1+h)-f(1))/h,h=0);
These commands can be summarized as follows.
- The D
command acts on a function.
- The diff command acts on an expression or a function and
differentiates that expression with respect to a variable specified by the user.
When you use the D operator to compute the derivative of a function, be careful with the parentheses. It is one of the only commands in Maple where the 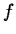 gets its own parentheses.
gets its own parentheses.
> f:=x->x^2;
> D(f)(x);
Finding the derivative at a specific 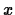 value is easy. (Again be careful of the parentheses.)
value is easy. (Again be careful of the parentheses.)
> D(f)(2);
The D operator CANNOT be used on expressions. To differentiate expressions, you need to use the diff command. Here is an example.
> p:=3*x+2;
> diff(p,x);
Remember the diff command can also be applied to functions. However, the syntax for plugging in an 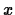 value is a little longer with the diff command. To compute the value of the derivative at a specific value of
value is a little longer with the diff command. To compute the value of the derivative at a specific value of 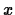 requires you to use the subs command. First, give the diff command a name so you can call it up in the subs command.
requires you to use the subs command. First, give the diff command a name so you can call it up in the subs command.
> pprime:=diff(p,x);
> subs(x=2,pprime);
Another option is to embed the commands.
>subs(x=2,diff(p,x));
Suppose you want to find the equaton of the line tangent to the graph of 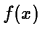 at the point
at the point 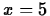 . This can be done in Maple using the point slope form of a line as shown below and remembering that you can embed commands inside each other. The line equation is
. This can be done in Maple using the point slope form of a line as shown below and remembering that you can embed commands inside each other. The line equation is
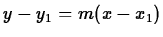 or
or
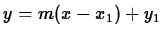
> tly:= D(f)(5)*(x-5)+f(5);
> plot([f(x),tly],x=0..10);
- For the function
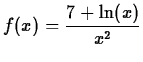
- A)
- Find the derivative of the functionusing the limit definition of the derivative, the diff command and then the D command (Make sure the output from all three are the same. You may need to use the simplify command.)
- B)
- And then use all three methods to find the slope of
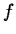 at
at 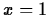 . (Again make sure the output from all three are the same. You may need to use the evalf command.
. (Again make sure the output from all three are the same. You may need to use the evalf command.
- Find the equation of the line tangent to the graph of the function
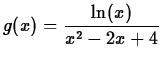 at
at 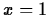 . Include a plot of the function and the tangent line on the same graph over the interval
. Include a plot of the function and the tangent line on the same graph over the interval
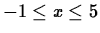 .
.
- For the function
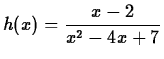 , find all points on the graph of
, find all points on the graph of 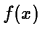 where the tangent line is horizontal.
where the tangent line is horizontal.
- A)
- Plot the function and state how many points you are looking for.
- B)
- Find the
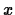 values.
values.
- C)
- Find the
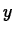 values. Then state in text the points where there is a horizontal tangent line. State your answers in decimal form. (Remember in the text sentence to use two decimals, rounding correctly.)
values. Then state in text the points where there is a horizontal tangent line. State your answers in decimal form. (Remember in the text sentence to use two decimals, rounding correctly.)



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2011-08-17
![]() gets its own parentheses.
gets its own parentheses.
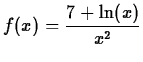
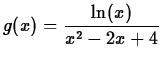 at
at 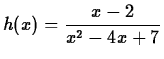 , find all points on the graph of
, find all points on the graph of