Subsections

• • Implicit Differentiation
  
  
• Plotting and solving implicitly
• Exercises

Implicit Differentiation

Implicit Differentiation

The implicitdiff command can be used to find derivatives of implicitly defined functions. Suppose we wanted to use implicit differentiation to find $$\frac{dy}{dx}$$ for the relation

$$x^2y^2+y^3=0$$

Then we first define our relation and give it a label for later use.

> f:=x^2*y^2+y^3=0;

Note that the expression syntax is used as the equal sign is entered as part of the command. You cannot use function notation! The syntax of the implicitdiff command is shown by the following example.

> implicitdiff(f,y,x);

The result of the command is the derivative, $$\frac{dy}{dx}$$. The first argument is the relation that you want to differentiate implicitly. We were careful to use an equation for this argument, but if you just give an expression for this argument, Maple assumes you want to set this expression equal to zero before differentiating. The second argument to the implicitdiff command is where you tell Maple what the dependent variable is. The remaining argument is to specifying the derivative you want.

To compute numerical values of derivatives obtained by implicit differentiation, you have to use the subs command. For example, to find the value of $$\frac{dy}{dx}$$ at the point $(1,-1)$ you could use the following command.

> subs([x=1,y=-1],implicitdiff(f,y,x));

Plotting and solving implicitly

First of all if you are going to plot implicitly you need to load the plots package.

> with(plots):

The implicitplot, solve, and fsolve commands have syntax similar to what you are familiar with. Just remember that you are dealing with two variables $x$ and $y$. When graphing the two equations in implicitplot you must specify the domain AND range.

> f := x^2*y^2+y^3 = 0;g := x^2*sin(y) = 1;
> implicitplot([f,g],x=-10..10,y=-10..0);

You can add options to the plot command to make the picture more clear. Execute the following commands to see the improvements.

> implicitplot([f,g],x=-10..10,y=-10..0,numpoints=10000);
> implicitplot([f,g],x=-10..10,y=-10..0,numpoints=10000,color=[``Aqua'',
''Magenta'']);
> implicitplot([f,g],x=-10..10,y=-10..0,numpoints=10000,color=[``Aqua'',
''Magenta''],scaling=constrained);

To find where the graphs intersect you can use the solve or fsolve command. Since you need to solve two equations with two unknowns you need to solve simultaneously. Simply use curly brackets in the commands to do this.

> a := fsolve({f, g}, {x = -5 .. 0, y = -5 .. 0});
> b := fsolve({f, g}, {x = -5 .. 0, y = -5 .. 0});
> c := fsolve({f, g}, {x = 0 .. 5, y = -5 .. 0});
> d := fsolve({f, g}, {x = 0 .. 5, y = -10 .. 5});

You could then use these points to find the slopes of either function.Then you could use the points and slope values to find the tangent lines. Pay particular attention to how the output-variable name a is used in the commands!!!!

> afslope := subs(a, implicitdiff(f, y, x));
> agslope := evalf(subs(a, implicitdiff(g, y, x)));
> afline := afslope*(x-a[1])+a[2];
> agline := agslope*(x-b[1])+b[2];
> implicitplot([g, f, afline, agline], x = -10 .. 10, y = -10 .. 5,
 numpoints = 10000, color = ["Aqua", "Magenta", "DarkOliveGreen", "Blue"],
 scaling = constrained);

Exercises

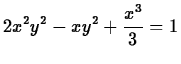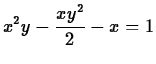1. Enter the following equations as expressions in Maple: $$2x^2y^2-xy^2+\frac{x^3}{3}=1$$ and the vertical line $x = -1$.

   A)

   Plot the two equations experimenting with the domain and range and the options to get a good picture of the intersections.

   B)

   Using the solve command find the y values of the interesction points.

   C)

   Find the slope of the first equation at the intersection point with the positive y value.

   C)

   State the intersection point and its slope. Then looking at the graph give at least two reason that the slope value seems to make sense.

2. Given the relation $$x^2y-\frac{xy^2}{2}-x=1$$,

   A)

   Plot the graph of the relation over the interval $-5 \leq x \leq 5$ and $-5 \leq y \leq 5$.

   B)

   Using fsolve commands, find the points where the equation has horizontal tangents. Remember you are solving the derivative and the equation simultaneously so you will need to use curly brackets. State your points in text.

   C)

   Plot the equation and the horizontal tangent lines. (Remember, these are horizontal lines so the equations should be simple.)