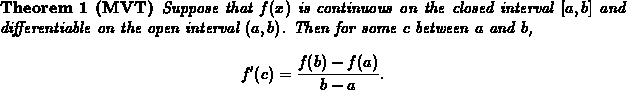
The mean value theorem is one of the most important and useful theorems from calculus. Before stating it, here is a (rather silly) application of it.
Just after you get on the Pike by Auburn, you pass a car pulled over by the highway patrol. Feeling glad that it isn't you, and relatively safe because you have a radar detector, you blast on by. One hour and eighty miles down the road, however, another patrolman pulls you over. You're not worried, because your detector had warned you to slow down. Imagine your shock, however, when he proceeds to write you a ticket for going 80 miles per hour! When you protest, he tells you that the patrolman at Auburn had radioed your position ahead. He then claims that since your average speed was eighty, the MVT says you must have been going eighty at least once in your journey. Then you see the ``MathNet'' patch on his uniform, and you really start to get that sinking feeling.
Mathematically, the MVT can be stated as follows.
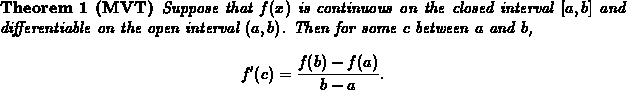
Geometrically, the MVT says that for at least one point strictly
between a and b, the slope of the tangent line to the graph of
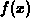is equal to the slope of the straight line between the two
points 
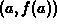and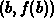 
. (Note: This line is often called the
secant line between a and b.) Obtaining a formula for the secant
line isn't hard, but to cut down on the amount of Maple drudgery, a
procedure, called secantline has been written that does this for you.
The secantline command takes three arguments. The first is a
function or expression, the next one is the base point, and the third
is the increment, b-a.
Before you can use this procedure, you must first load it using the
with(CalcP) command, as shown in the following example session.
> with(CalcP):
> f := x -> x^3;
> g := secantline(f(x),x=-1,2);
> plot({f(x),g},x=-1..1);
Looking at the graph displayed in the previous example, you should be
able to see that there are two values of x between x=-1 and x=1
where the slope of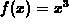 
is the same as the slope of the secant
line between the two points 
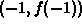and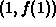 
.
To find these values, we need to solve for the values of x in the
interval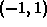 
where the derivative, 
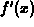, is equal to the slope
of the secant line, which is 1 in this example. Maple
commands to do this, and plot the two tangent lines are shown
below. In this case the solve command finds both solutions. Note
the use of the label sol and the notation sol[1] and
sol[2] to access the two roots.
> sol := solve(diff(f(x),x)=1,x);
> plot({f(x),g,tangentline(f(x),x=sol[1]),
tangentline(f(x),x=sol[2])},x=-1..1);
The solve command can't always do the job if the function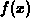 
is complicated. When the solve command fails, there is no output
from the command, as shown in the example below. In this case, use the
fsolve command instead, as shown below.
> f := x -> sin(x^2);
> g := secantline(f(x),x=4,1);
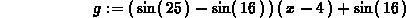
> plot({f(x),g},x=4..5);
> solve(diff(f(x),x)=diff(g,x),x);
> fsolve(diff(f(x),x)=diff(g,x),x=4..5);
It is important to restrict the x interval in the
fsolve command to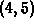 
in this case, because the equation
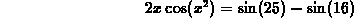
has an infinite number of solutions. In fact, there are three
solutions to this equation in the interval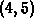 
. The fsolve
command given above found one of them. The other two can be found by
restricting the range in the fsolve command to an interval that
includes only the desired root. To do this, you need to determine
approximately where the roots are. Looking at the graph of the function
and the secant line is probably the best way to do this - just look
for points on the
curve where the slope of the tangent line is the same as the slope of
the secant line.
If you do this for the previous example,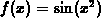 
, you
should be able to recognize that one of the roots is in the interval
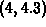. Using this interval in the fsolve command produces
the following results.
> fsolve(diff(f(x),x)=diff(g,x),x=4..4.3);
There is nothing special about the interval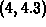 
; any other
interval that included the root at 
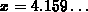, but didn't
include any other roots would have worked. That is, the interval
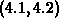would have worked equally as well, but the interval
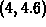is not a good choice because it includes two roots.