-
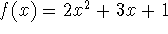 with a = 2 and a = -3.
with a = 2 and a = -3.
-
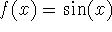 with a = 0 and
with a = 0 and 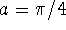 .
.
-
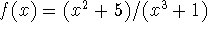 with a = 2 and a = 1.
with a = 2 and a = 1.
Suppose that ![]() and
and ![]() . Determine if the
following statements are true or not.
. Determine if the
following statements are true or not.
-
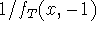 is tangent to 1/f(x) at x=-1.
is tangent to 1/f(x) at x=-1.
-
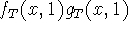 is tangent to f(x)g(x) at x=1.
is tangent to f(x)g(x) at x=1.
-
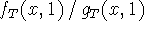 is tangent to f(x)/g(x) at x=1.
is tangent to f(x)/g(x) at x=1.
-
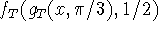 is tangent to
is tangent to 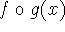 at
at 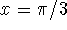 .
.