Exercises

1. Consider 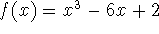and let r = 25. First let 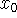be 1.414. What root is found? Next let 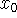be 1.145. What root is found? Why do two initial guesses so close together lead to different roots? Use your knowledge of the explanation of how Newton-Raphson works to answer this part of the problem.
2. Use Newton-Raphson to find all points at which the graph of the function
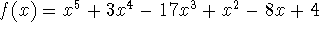   has a horizontal tangent line. Explain why you can be sure that you have indeed found all such points.
3. Consider 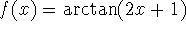, let 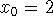and r = 30. Discuss what happens. Explain why this behavior occurs. Are there any values (that are not roots) that lead to a root? Find all roots of f(x) = 0. Again note that Newton-Raphson can be very sensitive to the initial guess that is used.
4. Construct a polynomial function g(x) of degree 5 or greater that has no real roots. Explain why you are sure it has no real roots. Let r = 20. Select a value for 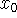and run Newton. Try a different value for 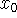(one not close to the original value) and run Newton. Discuss the output for these two runs. Describe what happens.