

Note:All example commands given in this write-up and the output from them should be included in your lab report.
Maple knows how to take many derivatives. Its main commands for doing this are D and diff. D is designed to differentiate functions, whereas diff is for differentiating expressions. However, if proper notation is used, diff can also be used with functions. To review the difference between a function and an expression, check the two examples below. The f statement defines a function, the g statement defines an expression.
> f:=x->x^2+7*x+5;
> g:=x^3-5*x+8;
Here are some examples that show how D and diff work. Check the difference between these two commands.
> D(sin);
> D(sin)(x);
Also, check these two.
> D(f);
> D(f)(x);
Carefully consider these.
> diff(g,x);
> diff(f(x),x);
See what happens with these.
> diff(g(x),x);
> diff(f,x);
After the last four examples, you should be convinced that proper notation is very important in doing derivatives in Maple.
Maple can also do higher derivatives. Check these commands.
> diff(g,x$2);
> diff(f(x),x$2);
The $ sign is used to indicate repeated differentiation, the number following it tells how many times the function or expression is to be differentiated. D will also do repeated differentiation.
> (D@@2)(f)(x);
More information on diff and D can be obtained through Maple help screens.
Maple can be used to perform composition of functions (Note: functions, not expressions). The symbol for composition is @. Try these commands
> (f@f)(x);
> simplify(");
> h:=x->x^3+x^2-3*x+4;
> p:=x->8*x+6;
> (f@h@p)(x);
> simplify(");
> (p@h@f)(x);
> simplify(");
Are 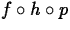 and
and 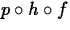 the same?
the same?
The implicitdiff command can be used to find derivatives of implicitly defined functions. The syntax is as follows
> implicitdiff(f,y,x);
where f is an expression or equation, y is the dependent variable and x is the independent variable. Thus the command as just stated would compute 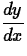 . If f is given as an expression Maple will assume that the implicit equation is f = 0. Check the results of the following commands.
. If f is given as an expression Maple will assume that the implicit equation is f = 0. Check the results of the following commands.
> f:=x^2*y^2+y^3;
> implicitdiff(f,y,x);
> g:=x^2+y^3=1;
> implicitdiff(g,y,x);
Second derivatives can also be taken with implicitdiff. The following command computes 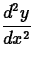 .
.
> implicitdiff(g,y,x,x);
Maple also has a command for plotting implicitly defined functions. It is in the package plots which must be called before using the command.
> with(plots);
> implicitplot(x^2-y^2=1,x=-3..3,y=-3..3);
- 1.
- Find an equation of the line tangent to the graph of
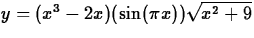 at the point (2,0). (Note that Maple has a sqrt function.)
at the point (2,0). (Note that Maple has a sqrt function.)
- 2.
- Find the third derivative of
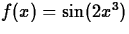 evaluated at
evaluated at 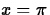 .
. - 3.
- Consider the function
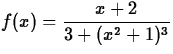 . Find the points at which the graph of this function has a horizontal tangent line. (The numer command could be useful here.) Use plot to graph the function. What geometric property seems to be indicated by a horizontal tangent line?
. Find the points at which the graph of this function has a horizontal tangent line. (The numer command could be useful here.) Use plot to graph the function. What geometric property seems to be indicated by a horizontal tangent line?
- 4.
- Consider the function
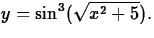
- (a)
- In order to take the derivative of the given function by using the Chain Rule, it is necessary to picture the function as the composite of several functions. Open a text section and explain how that is done for this problem.
- (b)
- Use Maple to take the composite of the functions you found in (a). Make sure this composite really gives the original function.
- (c)
- Open a text section and explain how the derivative is found by means of the Chain Rule.
- (d)
- Check your answer in (c) by using Maple to get the derivative.
- 5.
- Consider a function y that is implicitly defined by y5 - 3x2y + x3 = -1.
- (a)
- Attach a handwritten page on which you find
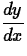 .
. - (b)
- Use Maple to check the accuracy of your work.
- (c)
- Find an equation of the line tangent to the graph of the function at the point (1,1).
Labs and Projects for Calculus using Maple
This document was generated using the
LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 1 lab_template.tex.
The translation was initiated by Christine M Palmer on 9/23/1997


Christine M Palmer
9/23/1997
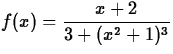 . Find the points at which the graph of this function has a horizontal tangent line. (The numer command could be useful here.) Use plot to graph the function. What geometric property seems to be indicated by a horizontal tangent line?
. Find the points at which the graph of this function has a horizontal tangent line. (The numer command could be useful here.) Use plot to graph the function. What geometric property seems to be indicated by a horizontal tangent line?
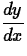 .
.