Exercises

1.

Consider f(x) = x⁴ - 16x - 12 and let r = 32. First let x₀ be 1.587. What root is found? Next let x₀ be 1.588. What root is found? Is a root really found? Why do two initial guesses so close together lead to different roots? Use your knowledge of the explanation of how Newton-Raphson works to answer this part of the problem.

2.

Use Newton-Raphson to find all points at which the graph of the function
f(x) = x⁵ + 3x⁴ - 17x³ + x² - 8x + 4 has a horizontal tangent line. Explain why you can be sure that you have indeed found all such points.

3.

Consider 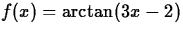$f(x) = \arctan(3x-2)$, let x₀ = 2 and r = 30. Discuss what happens. Explain why this behavior occurs. What is the signficance of the numbers that appear? Find all numbers which when used as x₀ will lead to a root. Hand in appropriate printouts. Again note that Newton-Raphson can be very sensitive to the initial guess that is used.

4.

Let f(x) = 3x⁴ - 4x³ - 84x² + 288 x + 732. Let x₀ = 2 and r = 10. Run Newton. What causes the result you get to occur? Explain this in terms of the Newton-Raphson process.

5.

Construct a polynomial function g(x) of degree 5 or greater that has no real roots. Explain why you are sure it has no real roots. Let r = 20. Select a value for x₀ and run Newton. Try a different value for x₀ (one not close to the original value) and run Newton. Discuss the output for these two runs. Describe what happens.