


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to calculate derivatives using the diff command and the D command in Maple.
Maple knows how to take many derivatives. Its main commands for doing this are D and diff. D is designed to differentiate functions, whereas diff is for differentiating expressions. However, if proper notation is used, diff can also be used with functions. To review the difference between a function and an expression, see the two examples below. The 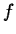 statement defines a function, the
statement defines a function, the 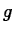 statement defines an expression.
statement defines an expression.
> f:=x->x^2-3*x+1;
> g:=x^2+5*x-2;
Here are some examples that show how D and diff work for the function 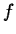 and the expression
and the expression 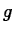 .
.
> D(f);
> D(f)(x);
> diff(f(x),x);
> diff(g,x);
Note that the output for D(f) is the only one above that has an arrow in it. This means that if you assign the output of D(f) to a label, the derivative can be used as a function in Maple whereas all other outputs when given a label would have to be used as expressions. The examples below show how this works for 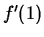 and
and 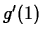 .
.
> df := D(f);
> df(1);
> df2 := D(f)(x);
> subs(x=1, df2);
> df3 := diff(f(x),x);
> subs(x=1, df3);
The D command and the diff command do not require the function or expression to be entered first. Here are some other examples of how these commands can be used.
> D(sin);
> D(sin)(x);
> D(sin)(Pi/2);
> diff(cos(x),x);
Finding the equation of a tangent line to a function at a given point 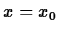 can be done using the point-slope form of a line.
can be done using the point-slope form of a line.
Where 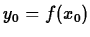 and
and 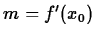 .
.
This can be done rather easily in Maple and we can even plot  and the tangent line on the same graph. See how this can be done for the tangent line to
and the tangent line on the same graph. See how this can be done for the tangent line to
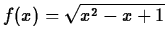 at
at 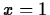 .
.
> f := x-> sqrt(x^2-x+1);
> y_tan := f(1) + D(f)(1)*(x-1);
> plot({f(x),y_tan}, x=0..2);
- Compute the derivatives of the following functions using both the diff command and the D operator for each function.
-
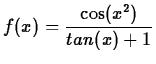
-
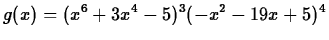
- Find the equation of the tangent line to
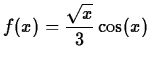 at the point where
at the point where 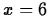 . Include a plot of the function and the tangent line on the same graph.
. Include a plot of the function and the tangent line on the same graph.
- Find all points on the graph of
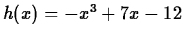 where the slope is equal to -1. Don't forget that a point includes both the
where the slope is equal to -1. Don't forget that a point includes both the 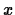 and
and 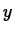 coordinates.
coordinates.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina Solitro
2001-11-27
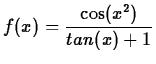
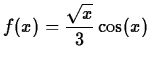 at the point where
at the point where