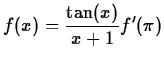Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to calculate limits using Maple and to find derivatives using the definition of the derivative.
Limits of functions and expressions can be computed in Maple using the limit command. The syntax of the limit command used to evaluate
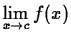 , using Maple is:
, using Maple is:
> limit(expression or function, x=c);
Notice that the first argument in the parentheses is the expression or function that you are taking the limit of; the second is the value that 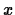 is approaching. You can type the expression directly into the limit command or another approach is to first define the expression or function with a label in Maple and use the variable name within the limit command. Below are some examples of each method.
is approaching. You can type the expression directly into the limit command or another approach is to first define the expression or function with a label in Maple and use the variable name within the limit command. Below are some examples of each method.
> limit(x^2+8*sin(-3*Pi*x), x=1/2);
> f:=x->(cos(x)-1)/x;
> limit(f(x),x=0);
If the limit exists, Maple can usually find it. In cases where the limit doesn't exist, such as
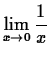 or
or
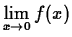 where
where
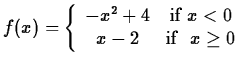 , Maple gives the answer undefined. Look at the plots of the functions to see why the limits are undefined.
, Maple gives the answer undefined. Look at the plots of the functions to see why the limits are undefined.
> limit(1/x,x=0);
> plot(1/x,x=-5..5,y=-10..10);
> p := piecewise(x<0,-x^2+4,x>=0,x-2);
> plot(p,x=-5..5);
> limit(p,x=0);
Another reason that a limit may not exist at a particular point is because of oscillations. For instance, the limit as 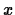 approaches 0 of
approaches 0 of
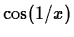 is undefined. To get a better idea of why, look at the plot. When evaluating the limit using Maple, the result is the range -1..1. When the limit doesn't exist, but the expression or function is bounded, this is the type of answer that Maple will give.
is undefined. To get a better idea of why, look at the plot. When evaluating the limit using Maple, the result is the range -1..1. When the limit doesn't exist, but the expression or function is bounded, this is the type of answer that Maple will give.
> plot(cos(1/x),x=-2..2);
> limit(cos(1/x),x=0);
Maple also can find one-sided limits. Suppose that you want to find the limit as 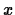 approaches 0 from the right for the function
approaches 0 from the right for the function
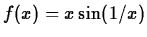 .
.
> f:=x->x*sin(1/x);
> limit(f(x),x=0,right);
Similarly, you can evaluate one-sided limits from the left by replacing the second argument with the word left.
The derivative of a function 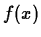 , often written
, often written 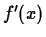 , is defined by the following limit.
, is defined by the following limit.
When using the definition to compute a derivative in Maple, it is easiest to first define the function 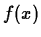 . You can then find the difference quotient of
. You can then find the difference quotient of 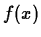 and take the limit as
and take the limit as 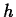 approaches 0 in either one or two steps. Both examples are shown below.
approaches 0 in either one or two steps. Both examples are shown below.
> f := x -> x^2+3*x+5;
> DQ:=(f(x+h)-f(x))/h;
> derivative:=limit(DQ,h=0);
To evaluate the derivative at a given x value, you can use one of two methods. Both are given below for 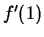 .
.
> subs(x=1,derivative);
> limit((f(1+h)-f(1))/h,h=0);
- Use Maple to evaluate each of the limits given below. If the limit exists, state the limit. If the limit does not exist, explain why. A plot may be necessary to support your answer.
-
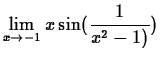
-
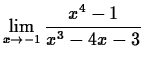
-
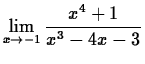
- State whether or not the limit
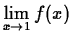 of the piecewise defined function
of the piecewise defined function
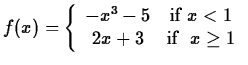 exists or not and support your answer using one sided limits.
exists or not and support your answer using one sided limits.
- Find the derivative of each function below using the definition of the derivative. Also, evaluate the derivative at the given value.
-
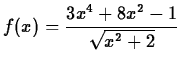 ,
, 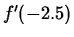
-
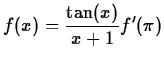



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina Solitro
2001-11-13
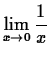 or
or
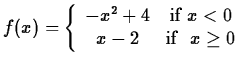 , Maple gives the answer undefined. Look at the plots of the functions to see why the limits are undefined.
, Maple gives the answer undefined. Look at the plots of the functions to see why the limits are undefined.
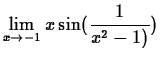
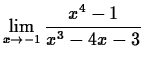
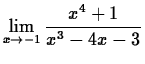
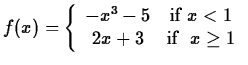 exists or not and support your answer using one sided limits.
exists or not and support your answer using one sided limits.
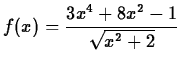 ,
,