


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to introduce you to the basics needed in
any Maple lab. The main topics include: assigning labels, defining
expressions, defining functions and plotting.
Suppose you want to assign a constant value to a variable name.
Assigning labels is done by choosing a variable name followed by :=
and then the value to be assigned to that variable name. For example,
to let myname=1.5, you can type:
> myname := 1.5;
Once you hit return after this Maple line, any time the string of
characters myname is used, it will have the value of 1.5.
Note the use of the colon in front of the equal sign. This is
necessary for assignment and if you forget the colon, Maple will not
give an error message. It will appear as if you correctly assigned
the value 1.5 to the label myname, however when you try to
use myname again in the worksheet, it will not have the value
1.5. Reusing variable names within the same lab is not recommended.
It can be done, however, Maple will only store in its memory the last
value that you assigned to the variable. So, if you go back to work
on a previous problem with the same variable and forget to re-execute
the old value, you could get some incorrect answers. Even if you do
it correctly, sometimes Maple keeps a value in memory even though
you've deleted the Maple line and tried to re-assign it. The best way
to reuse a variable is to "clear" its memory for that variable. You
can try the next example to see how this works.
> myname;
> myname := 'myname';
> myname;
Once you have cleared the variable, you are free to use it again.
Another thing to keep in mind is that if you close your Maple
worksheet for any reason and reopen it, none of the commands will be
stored in memory until you re-execute each command by hitting return
after each of the Maple lines. This can also be done by clicking on
the Edit menu and choosing Execute worksheet,
however, this could be time consuming if there are a lot of plots in
the worksheet.
Expressions such as 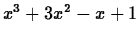 can be entered in a similar way to
variable assignment. Choose a variable name to represent the
expression and assign the expression to the variable as follows.
can be entered in a similar way to
variable assignment. Choose a variable name to represent the
expression and assign the expression to the variable as follows.
> expr1 := x^3+3*x^2-x+1;
Note that in the expression above, there is an asterisk between 3 and
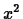 . A common mistake is to write two functions next to each other
without the "*" symbol. This would give incorrect results when using
this expression since Maple doesn't understand implied multiplication.
Suppose you want to enter the same expression stored in expr1
above, but as a function of
. A common mistake is to write two functions next to each other
without the "*" symbol. This would give incorrect results when using
this expression since Maple doesn't understand implied multiplication.
Suppose you want to enter the same expression stored in expr1
above, but as a function of 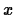 . In Maple, you would type
. In Maple, you would type
> f := x-> x^3+3*x^2-x+1;
Below is how ``NOT'' to enter a function:
> f(x) := x^3+3*x^2-x+1;
The difference between expressions and functions are first the
obvious, that expressions do not have to satisfy the definition of a
function in the sense that for each number in the domain, there is a
unique number in the range. A function may be defined as an
expression, but not all expressions can be defined as functions. The
differences in Maple are numerous as you will see below when we
evaluate the expression or function for a given value and when we use
the plot command.
In order to evaluate an expression at a given value of 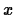 , you must
use the subs command. For example, if we wanted to evaluate
the expression expr1
, you must
use the subs command. For example, if we wanted to evaluate
the expression expr1 at
at 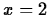 and at
and at
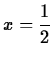 , the examples below show how this can be
done
, the examples below show how this can be
done
> subs(x=2,expr1);
> subs(x=2.,expr1);
In the subs command, the first argument tells Maple what you
would like to substitute in for 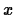 . The second argument tells Maple
what expression you are substituting into. Note the difference in
outputs when a whole number is entered compared to a decimal. Here
are a few more examples of evaluating expressions.
. The second argument tells Maple
what expression you are substituting into. Note the difference in
outputs when a whole number is entered compared to a decimal. Here
are a few more examples of evaluating expressions.
> subs(x=a+h,expr1);
> subs(theta=Pi,sin(theta)*cos(theta));
In Maple, functions are much easier to evaluate than expressions. In
order to evaluate the function
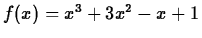 at
at 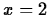 , then
simply type
, then
simply type
> f(2);
Here are a few more examples of evaluating functions.
> f(a+h);
> f(Pi);
> evalf(f(Pi));
Note the use of the evalf command in the last example above.
This command is used when we want Maple to output the answer in
decimal form. If this command is not used, the output to your Maple
commands will be calculated analytically, where as the evalf command
forces Maple to calculate the answers numerically. The evalf
command has one essential argument, however a second argument can be
added in order to tell how many digits we want to be in the answer.
> evalf(Pi,100);
The following example shows how the Maple plot command is
used to plot a function of one variable.
> f := x-> x^2;
> plot(f(x),x=-2..2);
The plot command above has two essential arguments. The
first argument is the function(s) or expression(s) that you want to
plot. The function or expression can be typed in before the plot
command or you can simply type it in as the first argument. The
second argument is the range of numbers for the 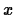 -axis. The
plot command allows you to add additional optional arguments
as well. For instance, you may want to also restrict the y-axis range
or add a title to your plot.
-axis. The
plot command allows you to add additional optional arguments
as well. For instance, you may want to also restrict the y-axis range
or add a title to your plot.
> plot(x^2,x=-2..2,y=-5..5,title=`My First Plot`);
This particular command allows you to add arguments, but if you were
to leave off one of the essential arguments, you will get an error
message. You can also plot more than one function or expression on
the same graph by enclosing them in curly braces ``{}'' and
separating them by commas. For example, we can plot 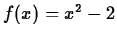 and
and
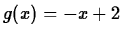 on the same graph.
on the same graph.
> f := x-> x^2-2;
> g := x-> -x+2;
> plot({f(x),g(x)},x=-4..4);
- Enter
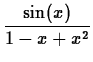 as an expression
and choose a variable name of your choice.
as an expression
and choose a variable name of your choice.
- Evaluate this expression at
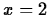 .
.
- Evaluate this expression at
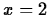 and give your answer in decimal form.
and give your answer in decimal form.
- Evaluate this expression at
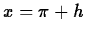 .
.
- Plot this expression over the
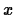 range
range
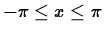 .
.
- Repeat exercise 1 by first defining
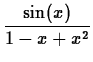 as a function.
as a function.
- Define
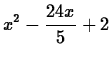 and
and 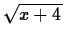 as
functions. Plot them both on the same graph. Estimate the two
intersection points by observing the plot. Plug each
as
functions. Plot them both on the same graph. Estimate the two
intersection points by observing the plot. Plug each 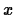 value back
into both functions to show that the
value back
into both functions to show that the 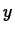 values are the same.
values are the same.



Next: About this document ...
Up: lab_template
Previous: lab_template
William W. Farr
2002-10-29
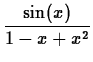 as an expression
and choose a variable name of your choice.
as an expression
and choose a variable name of your choice.
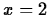 .
.
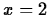 and give your answer in decimal form.
and give your answer in decimal form.
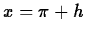 .
.
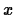 range
range
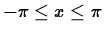 .
.
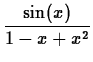 as a function.
as a function.
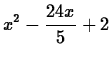 and
and 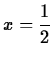 , the examples below show how this can be
done
, the examples below show how this can be
done