


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
Suppose that 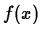 is a differentiable function and that
is a differentiable function and that 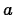 is some fixed number in the domain of
is some fixed number in the domain of 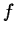 . We define the linear approximation to
. We define the linear approximation to 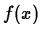 at
at
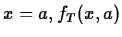 by the equation
by the equation
In this equation, the parameter 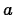 is called the base point, and
is called the base point, and 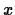 is the independent variable. You may recognize the equation as the equation of the tangent line at the point
is the independent variable. You may recognize the equation as the equation of the tangent line at the point 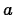 . It is this line that will be used to make the linear approximation.
For example if
. It is this line that will be used to make the linear approximation.
For example if 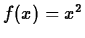 , then
, then 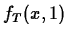 would be the line tangent to the parabola at
would be the line tangent to the parabola at 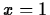
> f:=x->x^2;
> fT1:=D(f)(1)*(x-1)+f(1);
> plot({f(x),fT1},x=-1..3);
Obviously the two things the function and the tangentline have in common at 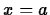 are their y-value and their slope.
Looking at the plot, the line will approximate the function exactly at the base point a and the approximation will be close if you stay close to that base point. To see how far off the approximation becomes on the given interval of the plot it is easy to see that the largest errors occur at the ends of the interval, i.e.
are their y-value and their slope.
Looking at the plot, the line will approximate the function exactly at the base point a and the approximation will be close if you stay close to that base point. To see how far off the approximation becomes on the given interval of the plot it is easy to see that the largest errors occur at the ends of the interval, i.e. 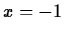 and
and 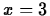 . Simply subtract the y-values to calculate the error.
. Simply subtract the y-values to calculate the error.
> abs(f(-1)-subs(x=-1,fT1));
> abs(f(3)-subs(x=3,fT1));
Notice that the error grows to four at each end of the interval.
How could you find an interval such that the greatest error will be a specific value? Think about this as it will appear in the exercises.
Two functions are said to be tangent at a point 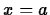 if their y-values are equal,
if their y-values are equal, 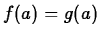 and if their tangent slopes are equal
and if their tangent slopes are equal 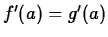 . For example, the functions
. For example, the functions 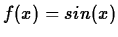 and
and 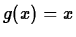 are tangent at
are tangent at 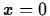 . Check their y-values and their derivatives at the given point.
. Check their y-values and their derivatives at the given point.
> f:=x=>sin(x);g:=x->x;
> f(0);g(0);
> D(f)(0);D(g)(0);
However, 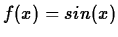 and
and 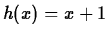 aren't tangent at
aren't tangent at 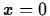 because even though they have the same slope they don't have the same y-value.
because even though they have the same slope they don't have the same y-value.
> h:=x->x+1;
> D(f)(0);D(h)(0);
> f(0);h(0);
- Given:
- Graph the three functions on the same plot using the intervals
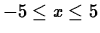 and
and
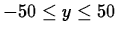
- Find the point where the functions intersect.
- Are any of the functions tangent to each other at the intersection point?
If so plot them with a small enough domain to show the tangent functions clearly.
- In your scientific studies you find that your results follow the function
- Plot your function twice, first on the interval
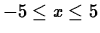 and second on the interval
and second on the interval
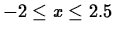
- You want to evaluate data around the base point
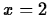 but you don't want to work with such a messy function. What is the linear approximation to this function at this base point? Plot the function and its linear approximation.
but you don't want to work with such a messy function. What is the linear approximation to this function at this base point? Plot the function and its linear approximation.
- You want to make sure that your linear approximation never is in error greater than 0.01. What is the interval of x data points that you can work with? (Use the fsolve command so you can find each interval endpoint) Plot the function and the linear approximation on the interval that you found.



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2004-11-30