Subsections

• Background
• Implicit Differentiaition
• Exercises

More on Differentiation

Background

Maple knows how to take many derivatives. Its main commands for doingthis are D and diff. D is designed to differentiate functions, whereas diff is for differentiating expressions. however, if proper notation is used, diff can also be used with functions. To review the difference between a function and an expression, check the two examples below. The f statement defines a function, the g statement defines an expression.

> f:=x->x^2+7*x+5;
> g:=x^3-5*x+8;

Here are some examples that show how D and diff work. Check the difference between these two commands.

> D(f)(x);
> diff(g,x);
> diff(f(x),x);

See what happens with these.

> diff(g(x),x);
> diff(f,x);

After the last four examples, you should be convinced that proper notation is very important in doing derivatives in Maple. Maple can also do higher derivatives. Check these commands.

> diff(g,x,x);
> (D@@2)(f)(x);

If you want to evaluate the derivative at a specific value of x, you can use the following

> D(f)(2);
> subs(x=3,diff(g,x));

Suppose you wanted to find the equation of the tangent line to the graph of f(x) at the point x = 5. This can be done in Maple using the point-slope form of a line as shown below. It is not necessary to label the command tanline; but giving the line a name makes it can easy to call it up if it is needed later.

> tanline := D(f)(5)*(x-5)+f(5);

More information on D and diff can be obtained through Maple help screens.

Implicit Differentiaition

The implicitdiff command can be used to find derivatives of implicitly defined functions. The syntax is as follows

> f:=x^2*y^2+y^3;
> implicitdiff(f,y,x);

where f is an expression or equation, y is the dependent variable and x is the independent variable. Thus the command as just stated would compute 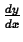$\frac{dy}{dx}$. If f is given as an expression Maple will assume the implicit equation is f = 0. Check the results of the following commands.

> g:=x^2+y^3=1;
> implicitdiff(g,y,x);

Second derivatives can also be taken with implicitdiff. The following command computes $\frac{d^2}{dx^2}$.

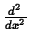> implicitdiff(g,y,x,x);

Maple also has a command for plotting implicitly defined functions. It is in the package plots which must be called before using the command.

> with(plots):
> implicitplot(x^2-y^2=1,x=-3..3,y=-3..3);

Exercises

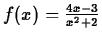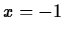1. Find the equation of the line tangent to the graph of the function $f(x)=\frac{4x-3}{x^2+2}$ at $x=-1$. Include a plot of the function and the tangent line on the same graph over the interval $-3 \leq x \leq 1$.
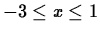2. Given 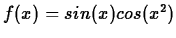$f(x) = sin(x) cos(x^2)$, evaluate the third derivative at 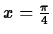$x = \frac{\pi}{4}$ using
   1. the D command.
   2. the diff command.
3. Consider the graph defined implicitly by the equation $x^2-xy+y^2=9$.
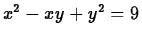   1. Enter the equation, calling it h.
   2. Use the implicitplot command to verify visually that the graph is an ellipse.
   3. Find the slopes to this curve at the two points where it intersects the x-axis labeling them m1 and m2. (Hint: You will first need to use the solve command to find the y-values) What can you tell about the tangent lines at these points given your answers for the slopes?
   4. Find the equations of the tangent lines to this curve at the two points where it intersects the x-axis labeling them t1 and t2. Renenber to enter the equations implicitly.
   5. Graph the ellipse and the two tangent lines on one graph.