


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to teach you how to use Maple commands for
computing derivatives.Use last week's lab to help you with the commands for this lab.
- Enter the expression
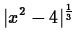 ,
,
- a)
- Compute the derivative and label the derivative using a variable name.
- b)
- Evaluate the derivative at
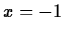 ,
,
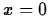 , and
, and
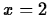 .
.
- c)
- Plot the expression over the interval
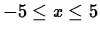 . Using this plot, can you explain why the expression was not differentiable at one of the
. Using this plot, can you explain why the expression was not differentiable at one of the 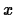 values given above?
values given above?
- Find the equation of the line tangent to the function
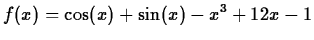 at
at 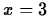 . When calculating the derivative at a point, use the
. When calculating the derivative at a point, use the 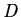 command. Include a plot of the function and the tangent line on the same graph over the interval
command. Include a plot of the function and the tangent line on the same graph over the interval
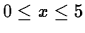 .
.
- For the same function
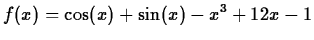 ,
,
- a)
- Plot
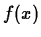 over the interval
over the interval
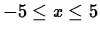 and state how many horizontal tangent lines to the graph there are.
and state how many horizontal tangent lines to the graph there are.
- b)
- Plot the derivative of
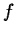 over the same interval. Explain how this supports your answer above.
over the same interval. Explain how this supports your answer above.
- c)
- Labeling each fsolve command, find the
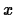 values where a horizontal tangent line is located. Find the corresponding
values where a horizontal tangent line is located. Find the corresponding
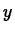 values. State in text all points on the graph of
values. State in text all points on the graph of 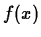 where the tangent line is horizontal.
where the tangent line is horizontal.
- The tangent line to a function at a particular value of x intersects the graph of the function at least once, at the point of tangency. However, the tangent line may intersect the graph at other points. In this problem, we investigate whether the tangent line at one point can also be tangent to the graph at another point. For example, consider the function
Find the point(s) where the tangent line at 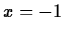 is also tangent to the graph.
is also tangent to the graph.



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2011-01-17
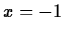 ,
,
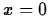 , and
, and
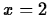 .
.
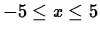 . Using this plot, can you explain why the expression was not differentiable at one of the
. Using this plot, can you explain why the expression was not differentiable at one of the  values given above?
values given above?
 over the interval
over the interval
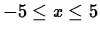 and state how many horizontal tangent lines to the graph there are.
and state how many horizontal tangent lines to the graph there are.
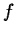 over the same interval. Explain how this supports your answer above.
over the same interval. Explain how this supports your answer above.
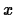 values where a horizontal tangent line is located. Find the corresponding
values where a horizontal tangent line is located. Find the corresponding
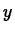 values. State in text all points on the graph of
values. State in text all points on the graph of 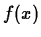 where the tangent line is horizontal.
where the tangent line is horizontal.