Exercises

1. For the functions and the values of a given below, go through the following steps:

• i. Find whether the $\lim_{x\rightarrow a}$ exists or not. If it does determine the limit.
• ii. For the limits that exist, find a value for $\delta$ that works for $\epsilon = 0.1$

$$1. f(x) = 2x+1, \;\; a=2$$

$$2. f(x) = \frac{2x+1}{x-1},\;\; a=1$$

$$3. f(x) = \frac{2x+1}{x-1},\;\; a=0$$

$$4. f(x) = \frac{\sin (x) + x^2}{x}, \;\; a=0$$

2. Determine the constants a and b that will make continuous the following function

$$f(x)=\left\{ \begin{array} {ll} x^2+a \;\; &\mbox{if} \; x<0... ...mbox{if}\; x=0 \\ bx+b \;\; &\mbox{if}\; x\gt\end{array}\right.$$

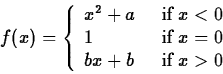
3. Define the function

$$f(x) = \left\{\begin{array} {ll} \displaystyle{\frac{\tan x}... ...{if} \; x\neq 0 \\ 1 \;\; &\mbox{if} \; x= 0 \end{array}\right.$$

Determine if the function is continuous at x=0

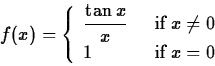
DUE DATE: FEBRUARY 1 (in class).