Exercises

1. Describe how the commands in the last set of Maple examples illustrate the definition of derivative as the limit of the slope of a secant line.

2. Specify the natural domain for each of the functions given below. Find the derivative of each of the functions both from the definition and using the D command.

i. f(x) = 2x²+1,

ii. f(x) = (x²+1)⁵

$$iii. f(x) = \cos (x^3)$$

$$iv. f(x) = \frac{\sin (1/x) + x^2}{x}$$

3. Define the function

$$f(x) = \left\{\begin{array} {ll} 2x^2+3\;\; &\mbox{if} \; x ... ...\sin({\pi x}/2)+3x\;\; &\mbox{if} \; x\geq 1 \end{array}\right.$$

Determine the derivative for all values of x for which it exists. Justify your result.

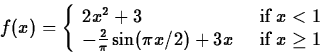
4. Determine the constants a, b and c that will make the following function differentiable

$$f(x)=\left\{ \begin{array} {ll} x^2+a \;\; &\mbox{if} \; x<0... ...=0 \\ \sin (x) - bx + c\;\; &\mbox{if}\; x\gt\end{array}\right.$$

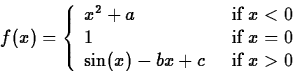
DUE DATE: FEBRUARY 8 (in class).