Exercises

First a short lesson in economics. The profit for a company is usually a function of the amount of some product sold. It is often the case that the rate of increase in profit is not constant. That is, one more mackerel sold does not always yield exactly 5 more clams in profit. Rather, it might be the case that the change in profit with respect to the number products sold might depend on that number, changing the rate of increase in profit as the output grows. So, one might consider P, the profit, to be a function of x, the amount of the product sold, and let dP/dx be the rate at which the profit changes (hopefully increases!) with sales. Marginal profit is the name usually given to this rate of change.

Suppose that the Hotshot Sneaker Company sells basketball sneakers, and that their marginal profit (in dollars per sneaker) is the following function of the number of sneakers sold, where x is the number of sneakers,

$$\frac{d P_h}{dx} = 8 x^{1/4} - 10 .$$

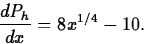
Suppose that Guys Shoes Shoe Company sells basketball sneakers also, and that their marginal profit is the following function of the number of sneakers sold, again with x as the number of sneakers,

$$\frac{d P_g}{dx} = 10 x^{1/3} -40.$$

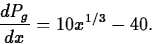
1.

After creating each of the marginal profit functions as Maple functions, plot them on the same graph over the range of 100 to 500 shoes. (We will assume that each company will sell at least 100 shoes.) Which company would you choose to invest in, assuming unlimited growth in sales? Why? Hint: You have already learned how to plot single plots in Maple. Use the Help option to find out how to graph multiple curves on the same plot.

2.

Consider finding the area under each of these curves, over the range from 100 to 200. What would be the units associated with your answer? Without actually finding the areas, what would your answers tell you? If you considered instead the range from 300 to 400, how would your interpretation differ?

3.

Approximate the area under each of the marginal profit curves over the range from 100 to 500. Use 3 subintervals, and experiment with both the leftsum and rightsum commands. Do your answers surprise you? Discuss.

4.

Choose one of the approximation methods (left, right, or midpoint), and approximate the area under each of the curves (on [100,500]) first using 10, 50, 100, and then 200 subintervals.

5.

Now find the exact area under each of the curves over the range from 100 to 500 using definite integrals.

6.

Now that you have the exact answer, return to using one of the approximation rules (left, right, mid, your choice) and find the minimum number of subintervals necessary to approximate the area to within two decimal places of accuracy for each of the curves. Discuss why you might have needed a different number of subintervals for the two curves.

7.

Why are you sure that a definite integral can be used for finding these areas?

8.

Find the average profit per sneaker made (for between 100 and 500 sneakers produced) for each of the companies.