Theoretical Notes

Exponential growth and decay. In many natural processes the rate of change of physical quantity (velocity, temperature, amount of money, electric current, whatever) is proportional to the current amount of the quantity. If we also know the amount present at time t=0, call it y₀, we can find y as a function of t by solving the following initial value problem:

Differential equation: 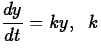$$\frac{dy}{dt} = ky,\;\; k$$ is a constant.
(1)
Initial conditions: y = y₀ when t = 0 .

If y is positive and increasing, then k is positive, and we use Eq. (1) to say that the rate of growth is proportional to what has already been accumulated. If y is positive and decreasing, then k is negative, and Eq. (1) is used to say that the rate of decay is proportional to the amount still left.

It is seen that the constant function y = 0 is a solution of Eq. (1). To find the non-zero solutions, the equation is solved in accordance with the known technique of separating variables and integrating (see [Varberg & Purcell, Calculus, p.372]). The solution of the initial value problem is

The constant y₀ is the value of the function at t=0. The constant k is called the growth rate in exponential growth (k >0) and the decay rate in exponential decay (k < 0). In a process that can be modeled by exponential functions, the rate constant k depends only on the process and the conditions under which it is carried out.

Some processes are described by differential equations similar to (1) but containing two or more constants characterizing some other circumstances in which these processes are carried out. Also, the initial conditions might be specified by more complicated expressions. The corresponding initial value problems lead to the solution having slightly different form, e.g., like (2) including a combination of additive and multiplicative constants. You will meet illustrations of that in the problems below.

In some applications, a quantity y demonstrates exponential growth or decay on a huge range. To make this quantity more convenient in handling, special scales involving logarithms are used. This allows to deal with the corresponding powers instead of actual values of y .

Relevant Maple Means. In order to enter the exponential and natural log functions, the exp and ln command should be used. The syntax of these commands is similar to that of sin and cos. For example, below it is shown how to enter the function f(x) = e^x and then evaluate it at x = 0.7.

  > f:=exp(x);

  > evalf(subs(x=0.7, f)); 

In the same manner, the function $g(x) = \ln(x)$ is used:

  > g := ln(x);

  > evalf(subs(x=0.7, f));

To simplify expression involving logarithms, use command simplify; it works as follows:

  > simplify(exp(a+ln(b*exp(c))));

The common logarithm is defined by function log10 = log[10], but log10 must be defined with the command readlib(log10) before use:

  > readlib(log10): log10(10000);

Maple manipulates with common logarithms the same way but may return expressions including natural logarithms.

The solve command is usually sufficient for solving most probelms encountered in your Calculus courses. This command comes in a couple of varieties, as shown below.

i.

Solve linear equation:

> solve (y=m*x+b,x);

ii.

Solve displaying result as an equation:

  > solve (34-2*x=12*x+6,x);

Plotting the two functions f(x) = e^x and $g(x) = \ln x$ on the same coordinate system illustrates an idea of the symmetry around the line y=x. All the three graphs can be plotted by the use of the following command:

  > plot(f,g,x, x=-4..4, y=-4..4);   

[height=3in, angle=-90]logpic.ps Fig. 1

In order to get a graph of a left-hand/right-hand side of an equation obtained after symbolic transformations and/or computations, first use commands lhs and rhs respectively. The example:

  > eq1 := A=b+c*exp(k*t): eq2 := subs(b=2.5,c=3,k=0.8,eq1):

  > rh2 := rhs(eq2):

  > plot(rh2, t=0..3);