


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to introduce you to Maple commands for
computing definite and indefinite integrals.
There are two main ways to think of the definite integral. The easiest
one to understand is as a means for
computing areas (and volumes). The second way the definite integral is
used is as a sum. That is, we use the definite integral to ``add
things up''. Here are some examples.
- Computing net or total distance traveled by a moving object.
- Computing average values, e.g. centroids and centers of mass,
moments of inertia, and averages of probability distributions.
This lab is intended to introuduce you to Maple commands for computing
integrals, including applications of integrals.
The basic Maple command for computing definite and indefinite
integrals is the int command. The syntax is very similar to
that of the leftsum and rightsum commands, except
you don't need to specify the number of subintervals.
Suppose you wanted to compute the following definite
integral with Maple.
The command to use is shown below.
> int(x^2,x=0..4);
Notice that Maple gives an exact answer, as a fraction. If you want a
decimal approximation to an integral, you just put an evalf
command around the int command, as shown below.
> evalf(int(x^2,x=0..4));
To compute an indefinite integral with Maple, you just leave out the
range for the limits of integration, as shown below.
> int(x^2,x);
Note that Maple does not include a constant of integration.
You can also use the Maple int command with functions or
expressions you have defined in Maple.
For
example, suppose you wanted to find area under the curve of the
function
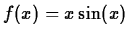 on the
interval
on the
interval ![$[0,\pi]$](img3.png) . Then you can define this function in Maple with
the command
. Then you can define this function in Maple with
the command
> f := x -> x*sin(x);
and then use this definition as shown below.
> int(f(x),x=0..Pi);
You can also simply give the expression corresponding to 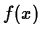 a
label in Maple, and then use that label in subsequent commands as
shown below. However, notice the difference between the two
methods. You are urged to choose one or the other, so you don't
mix the syntax up.
a
label in Maple, and then use that label in subsequent commands as
shown below. However, notice the difference between the two
methods. You are urged to choose one or the other, so you don't
mix the syntax up.
> p := x*sin(x);
> int(p,x=0..Pi);
If you want to find the area bounded by the graph of two functions, you should first plot both functions on the same graph. You can then find the intersection points using either the solve or fsolve command. Once this is done, you can calculate the definite integral in Maple. An example below illustrates how this can be done in Maple by finding the area bounded by the graphs of
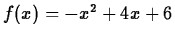 and
and 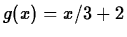 :
:
> f := x-> -x^2+4*x+6;
> g := x-> x/3+2;
> plot({f(x),g(x)},x=-2..6);
> a := fsolve(f(x)=g(x),x=-2..0);
> b := fsolve(f(x)=g(x),x=4..6);
> int(f(x)-g(x),x=a..b);
If a function 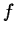 is integrable over an interval
is integrable over an interval ![$[a,b]$](img8.png) , then we
define the average value of
, then we
define the average value of 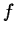 , which we'll denote as
, which we'll denote as 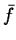 ,
on this interval to be
,
on this interval to be
Note that the average value is just a number. For example, suppose you
wanted to compute the average value of the function
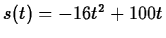 over the interval
over the interval
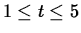 . The following Maple
command would do the job.
. The following Maple
command would do the job.
> int(-16*t^2+100*t,t=1..5)/(5-1);
- Use Maple to compute the following definite integrals.
-
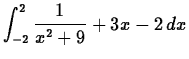
-
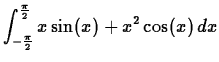
-
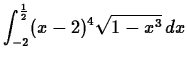
- Does the value of the integral in exercise 1(a) represent the area bounded by the integrand and the
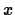 -axis over the interval
-axis over the interval
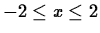 ? If so, explain why. If not, find the area.
? If so, explain why. If not, find the area.
- Find the area of the region bounded by the curves
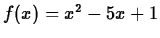 and
and
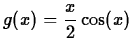 . Include a plot of the region.
. Include a plot of the region.
- Suppose the velocity in feet per second of a particle moving in
one dimension is given by
where 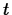 is the time in seconds. Find the average velocity of the particle over the interval
is the time in seconds. Find the average velocity of the particle over the interval
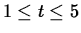 .
.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina Solitro
2001-11-14
![]() on the
interval
on the
interval ![]() . Then you can define this function in Maple with
the command
. Then you can define this function in Maple with
the command
![]() a
label in Maple, and then use that label in subsequent commands as
shown below. However, notice the difference between the two
methods. You are urged to choose one or the other, so you don't
mix the syntax up.
a
label in Maple, and then use that label in subsequent commands as
shown below. However, notice the difference between the two
methods. You are urged to choose one or the other, so you don't
mix the syntax up.
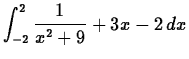
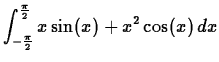
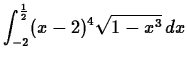
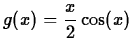 . Include a plot of the region.
. Include a plot of the region.