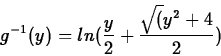Next: Exercises
Up: lab_template
Previous: Exponentials and Logarithms
Consider the functions 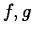 defined by
defined by
To be able to get an inverse the function must be one-to-one. You can plot the functions to get a hint as to whether they are invertible or not.
> f:=x->exp(x)+exp(-x);
> plot(f(x),x=-5..5);
> g:=x->exp(x)-exp(-x);
> plot(g(x),x=-5..5);
Both satisfy the vertical-line test but  is not invertible since it does not satisfy the horizontal-line test. Indeed
is not invertible since it does not satisfy the horizontal-line test. Indeed  is not one-to-one, for instance
is not one-to-one, for instance
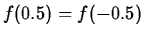 . From the plot it seems that the function
. From the plot it seems that the function 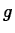 is one-to-one. In order to determine its inverse we solve for x.
is one-to-one. In order to determine its inverse we solve for x.
> solve(g(x)=y,x);
We observe that one of the solutions is not defined since the arguement of the logarithm can only be positive. Thus:
> ginv:=y->ln(y/2+sqrt(y^2+4)/2);
Let's look at the plot along with the line 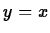 to see if our functions seem to make sense.
to see if our functions seem to make sense.
> plot({x,g(x),ginv(x)},x=-20..20,y=-20..20,scaling=constrained);
Let's check that we have computed the right inverse. By definition the composotion of the functions should be the line 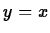 since an inverse is the reflection about this line.
since an inverse is the reflection about this line.
> g(ginv(y));
> simplify(%);
> ginv(g(x));
> simplify(%);
We are having difficulty getting 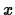 for the last composition. Think about what issue the computer has in dealing with this simplification as you will come across this in the exercises.
for the last composition. Think about what issue the computer has in dealing with this simplification as you will come across this in the exercises.



Next: Exercises
Up: lab_template
Previous: Exponentials and Logarithms
Jane E Bouchard
2004-12-06