


Next: Inverse Functions
Up: lab_template
Previous: lab_template
When the exponential function 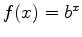 was introduced, (for
was introduced, (for 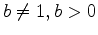 ) you saw that the function is increasing if
) you saw that the function is increasing if 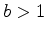 and decreasing if
and decreasing if 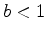 . You can observe the monotonicity by plotting
. You can observe the monotonicity by plotting 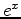 and
and 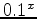 .
.
> plot(exp(x),x=-1..1);
> plot(0.1^x,x=-1..1);
The logarithmic function 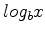 was introduced for
was introduced for 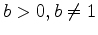 as the inverse of the exponential. The logarithm is therefore inreasing if
as the inverse of the exponential. The logarithm is therefore inreasing if 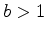 and decreasing if
and decreasing if 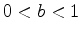 . Indeed you can plot
. Indeed you can plot 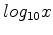 and
and 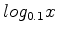 .
.
> plot(log[10](x),x=0.1..10);
> plot(log[0.1](x),x=0.1..10);
From the monotonicity properties you can compare two logarithms having the same base without computing their values:
We can also see what is the behavior of the logarithm of different bases by using the 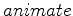 command. To get the animation to play, just click on the graph and click on the go button in the tool bar.
command. To get the animation to play, just click on the graph and click on the go button in the tool bar.
> with(plots):
> animate(log[b](x),x=0.1..10,b=1.1..10,frames=30);
> animate(log[b](x),x=0.1..10,b=0.01..0.1,frames=30);
From the monotonicuty properties you can see that for a fixed 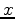 in the interval
in the interval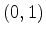 the logarithm increases with
the logarithm increases with 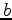 but for
but for 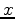 in the interval
in the interval 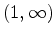 it decreases. As a result you can now compare logarithms with different bases without computing their values.
it decreases. As a result you can now compare logarithms with different bases without computing their values.
Here are some examples using Maple to solve logarithmic and exponential equations.
> solve(5^(x+1)+5^x+5^(x-1)=155,x);
> solve(log[5](2*x^2+2*x+5)=2,x);



Next: Inverse Functions
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2010-12-08