Subsections

• Exercises

Center of Mass

For symmetric objects, the balance point or center of mass is usually easy to find. For example, the balance point of an empty see-saw is the exact center. Similarly, the balance points for rectangles or circles are just the geometrical centers. For non-symmetric objects, the answer is not so clear, but it turns out that there is a fairly simple algorithm involving integrals for determining balance points.

We begin by restricting our attention to thin plates of uniform density. In Engineering and Science, this type of object is called a lamina. For mathematical purposes, we assume that the lamina is bounded by $x=a$, $x=b$, $y=f(x)$, and $y=g(x)$, with $g(x) \leq f(x)$. Then the book gives the following formulas for the coordinates $(\bar{x},\bar{y})$ of the center of mass.

$$\bar{x} = \frac{\int_a^b x (f(x)-g(x))\, dx}{\int_a^b f(x)-g(x)\, dx}$$

$$\bar{y} = \frac{1}{2} \frac{\int_a^b f(x)^2-g(x)^2\, dx}{\int_a^b f(x)-g(x)\, dx}$$

Note that the denominator of each coordinate is the same as finding area. This is called the mass. Therefore, let's look at the example from the integral lab where we found the area between $f(x)=-x^2+4x+6$ and $g(x)=x/3+2$:

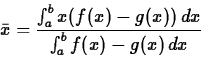
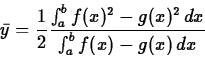
> f := x-> -x^2+4*x+6; 
> g := x-> x/3+2;
> plot({f(x),g(x)},x=-2..6);
> a := fsolve(f(x)=g(x),x=-2..0);
> b := fsolve(f(x)=g(x),x=4..6);
> mass:=int(f(x)-g(x),x=a..b);

We will call the integral mass instead of area and will use it in the coordinate formulas. Using labels can help you organize your calculations and avoid mistakes. Computing the mass separately also lets you check it. If you get a negative value for the mass, something is wrong and you have to check what you have done. A common mistake is reversing the order of the functions.

> xbar := int(x*(f(x)-g(x)),x=a..b)/mass;
> ybar := 1/2*int(f(x)^2-g(x)^2,x=a..b)/mass;

To check if the answer is reasonable you may plot the point.

> plot([f(x), g(x), [[xbar, ybar]]], x = -2 .. 6, style = [line, line, point], 
color = black,symbolsize=30);

Exercises

1. Find the coordinates of the center of mass of the lamina bounded by the curves $f(x)= 9-4x^2$ and $g(x)=6x\cos(x)$. Plot both curves on the same graph along with the point $(\bar{x},\bar{y})$ to see if your answer makes sense.

2. Find the coordinates of the center of mass of the lamina bounded by the curves $f(x)=-exp(x)+4$ and $ln(x^2+5)$. Plot both functions on the same graph along with the point $(\bar{x},\bar{y})$ to see if your answer makes sense.

3. Find the coordinates of the center of mass of the lamina bounded by the curves $f(x)=\frac{8}{7}x^4+0.1$ and $g(x)=x^6$. Plot both functions on the same graph along with the point $(\bar{x},\bar{y})$ to see if your answer makes sense.

4. Find the coordinates of the center of mass of the lamina bounded by the curves $f(x)=\sqrt{25-x^2}$, $g(x)=-(x+4)$ and $h(x)=(x-3)^3$. Plot the functions on the same graph along with the point $(\bar{x},\bar{y})$ to see if your answer makes sense.