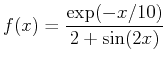 over the interval
over the interval
- A
- Plot
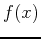 over the given interval.
over the given interval.
- B
- Plot the approximation of the solid of revolution using LeftDisk with 12 disks.
- C
- Plot the solid formed by revolving
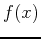 about the
about the 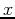 -axis.
-axis.
- D
- Find the exact volume of the solid of revolution using the RevInt command and label your output exact.
- E
- Find the number of subintervals needed to approximate the
volume of the solid of revolution about the
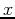 -axis using
LeftInt with error no greater than 0.1.
-axis using
LeftInt with error no greater than 0.1.
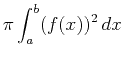 instead of the RevInt command.
instead of the RevInt command.
- A
- The volume of a sphere of radius
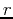 is
is
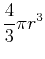
- B
- The volume of a cylinder of radius
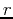 and height
and height 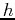 is
is 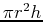 .
.
- C
- The volume of a right circular cone of radius
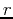 and height
and height 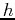 is
is
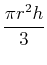
about the