-
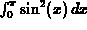
-
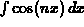 , where n is a positive constant.
, where n is a positive constant.
-
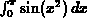
-
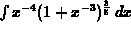
For Exercises 2-5, consider the function:
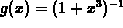 on
on 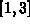
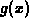 . Note that the
Maple command
. Note that the
Maple command
h:= diff(g(x), x$4);
defines h to be the 4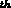 derivative of g.
derivative of g.
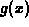 , what accuracy is
guaranteed by the Simpson's error bound formula? By the Trapezoidal
error bound formula? If values from the int command are assumed to be
correct, what accuracy was in fact achieved in each case?
, what accuracy is
guaranteed by the Simpson's error bound formula? By the Trapezoidal
error bound formula? If values from the int command are assumed to be
correct, what accuracy was in fact achieved in each case?
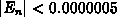 ). Compare the values
of n for each method, including the midpoint rule (See Lab 1,
exercise 3). What conclusion could you draw about the relative
accuracy of the three approximation methods?
). Compare the values
of n for each method, including the midpoint rule (See Lab 1,
exercise 3). What conclusion could you draw about the relative
accuracy of the three approximation methods?