


Next: About this document
Up: Introduction to Volumes
Previous: Background
- This exercise is intended to familiarize you with the
procedures revolve, RevInt,
LeftDisk and LeftInt as an approach to approximating the volume
of a solid of revolution using the disk method. Apply the four
commands as listed above to the function f defined by
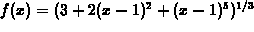 on the interval
on the interval 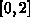 with n=10. Your
answer should include the two numerical values and references to the
two 3-dimensional plots.
with n=10. Your
answer should include the two numerical values and references to the
two 3-dimensional plots.
- The formula for the volume of a cone, namely,
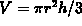 can be obtained by assigning the points
can be obtained by assigning the points 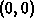 ,
, 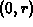 , and
, and 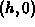 as the vertices of a right triangle and rotating that triangle about
the x-axis.
as the vertices of a right triangle and rotating that triangle about
the x-axis.
- Following a similar approach as above, derive the formula for
the volume of a frustrum of a cone. That is, a cone with the top cut
off parallel to the base.
- Show that your formula can be expressed in the traditional
handbook form:
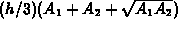 , where
, where 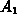 and
and
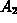 are the areas of the two bases.
are the areas of the two bases.
- A torus - a solid shaped like a doughnut - is generated by
revolving a circle about an axis that does not intersect the circle.
By rotating the circle
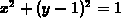 about the line y = 3,
print a plot of the torus which depicts its doughnut-like image and
compute its volume. Your answer should include the numerical value
for the volume and a reference to the 3-dimensional plot.
about the line y = 3,
print a plot of the torus which depicts its doughnut-like image and
compute its volume. Your answer should include the numerical value
for the volume and a reference to the 3-dimensional plot.
- A glass container is fashioned acording to the image obtained by
rotating the graph of the function g defined by
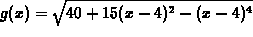 on the interval
on the interval 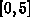 and x measured in
centimeters.
and x measured in
centimeters.
- Obtain a plot of the the container in an upright position. Be
sure to reference your plot.
- Determine the capacity of the container if filled to the brim.
- It is decided that Herky the minnow is to be allowed to use the
container as a fish bowl. When Herky is placed in the container
when it is filled to a depth of 4 cm, the depth increases to 4.5 cm.
If the water weighs 1 gm/cm
 , how much in ounces does Herky weigh?
, how much in ounces does Herky weigh?
In exercise 4, 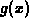 can also be expressed as
can also be expressed as 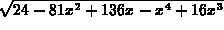 .
.



Next: About this document
Up: Introduction to Volumes
Previous: Background
Sean O Anderson
Wed Dec 6 09:46:40 EST 1995
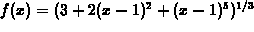 on the interval
on the interval 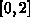 with n=10. Your
answer should include the two numerical values and references to the
two 3-dimensional plots.
with n=10. Your
answer should include the two numerical values and references to the
two 3-dimensional plots.
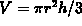 can be obtained by assigning the points
can be obtained by assigning the points 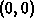 ,
, 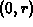 , and
, and 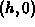 as the vertices of a right triangle and rotating that triangle about
the x-axis.
as the vertices of a right triangle and rotating that triangle about
the x-axis.
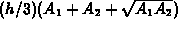 , where
, where 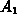 and
and
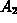 are the areas of the two bases.
are the areas of the two bases.
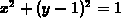 about the line y = 3,
print a plot of the torus which depicts its doughnut-like image and
compute its volume. Your answer should include the numerical value
for the volume and a reference to the 3-dimensional plot.
about the line y = 3,
print a plot of the torus which depicts its doughnut-like image and
compute its volume. Your answer should include the numerical value
for the volume and a reference to the 3-dimensional plot.
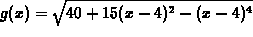 on the interval
on the interval 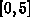 and x measured in
centimeters.
and x measured in
centimeters.
 , how much in ounces does Herky weigh?
, how much in ounces does Herky weigh?
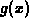 can also be expressed as
can also be expressed as 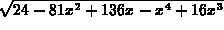 .
.