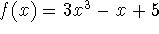Exercises

1. For each function listed below first look at plots constructed using rightbox and leftbox for n=5 and n=10, but do not include these plots in your report. Then, find the upper and lower sums (be sure to indicate which is which) with n = 50, 100, and 200. Based on this information alone, make a guess as to the value of A. Show the upper and lower sums that you found, and then explain the basis for your guess.
   1. on the interval [1,4].
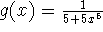   2. 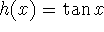on the interval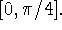 [1,2].
   3. on the interval
2. For each function given in Exercise 1, look at the results of middlebox for n = 5 and 10, but do not include these plots in your report. Find the midpoint approximation with n = 50, 100, 200. Now what would you guess is the value of A? Explain your guesses, and how and why they differ from what you guesses in Exercise 1. Show the midpoint sums that you found.
3. The following problems refer to the g(x) given in Exercise 1. Both questions below can be determined through the use of appropriate Maple commands. Note that the command

     > h:= diff(g(x), x, x);
   

   defines h(x) to be the second derivative of g(x). Also note that the solve command can be used with inequalities.

   1. If 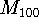is used to approximate A, what accuracy is guaranteed by the error bound formula? State what value of K you chose and explain how you picked it.
   2. What is a reasonable n to use if 5-place accuracy is desired? That is, if

      

4. Use the midpoint rule and one of the other rectangular rules to approximate the following integrals to four decimal places using the least number of subintervals. Your report should include the approximate values of the integrals and the minimum number of subintervals required for each method to achieve this accuracy.

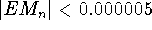
   An accuracy of four decimal places means that your result, rounded to four decimal places, does not change when you increase the number of subintervals further.

   1. 
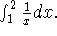
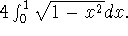   2. Does this turn out to be a familiar number to you? Discuss why.