- Find the area under the graph of
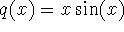 on the interval
on the interval 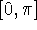 .
.
- Find the average value of the function
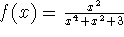 on the interval [-5,-1].
on the interval [-5,-1].
- Find the area between
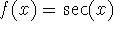 and
and 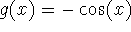 on the interval
on the interval 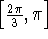 .
.
- Find the general antiderivative of
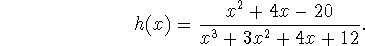
- Approximate I by
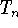 for n = 20, 60 and 100.
for n = 20, 60 and 100.
Approximate I by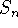 for n = 20, 60 and 100.
for n = 20, 60 and 100.
Approximate I by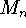 for n = 20, 60 and 100.
for n = 20, 60 and 100.
- In estimating error, the values M, K and B are often approximated by a number N that is an upper bound of M or K or B. Find such upper bounds of M, K and B for the integrand of I. Note that the Maple command
> h:=diff(g(x),x,x,x,x);
defines h to be the 4th derivative of a function g. You may also want to make use of the plot command.
- If n = 60, what accuracy in estimating I is guaranteed by the trapezoidal error formula? By the Simpson's error formula? By the midpoint error formula? If values from the int command are assumed to be correct, what accuracy was in fact achieved in each case?
- Write a paragraph summarizing your experience in this problem. (Feel free to run additional lines of Maple if you need to.) What approximation method seems to be the most accurate? Look at the error formulas for midpoint and trapezoidal approximations and decide, on the basis of these error statements, which method is likely to be more accurate for a given n. How much more accurate is the better method? Include at least one more insight you have gained from this exercise.
![]()