If we have a curve lying entirely on or above the x-axis, which is the
graph of a function f(x), and x is restricted to being between a
and b, then we may rotate it about the x-axis, generating a three
dimensional object; a solid of revolution.
For example, if the curve is simply f(x) = ax/h (a straight line)
and x is between 0 and h, we obtain a cone of height h and radius a.
If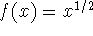 
and x is between, say, 0 and 1, we obtain a bowl
shaped object called a paraboloid. (Note the equation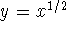 
is equivalent to 
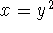, a parabola).
If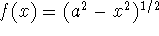 
and x is between -a and a,
we obtain a sphere of radius a (since the equation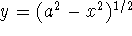 
is equivalent to 
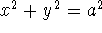, a circle of radius
a).
The textbook (p. 388) develops the formula that the volume of
the solid obtained by rotating about the x-axis is given by
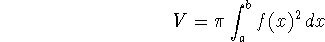
The volume is obtained by adding up volumes of cylindrical disks, while its surface area (p. 400) is given by
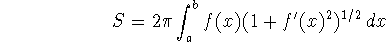
Note that both of these formulas are for rotating the graph of f(x) about the x-axis.