


Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
- 1.
- Use the Maple int command to work the following problems.
- (a)
- Find the average value of
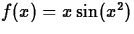 on
on ![$[0,\pi]$](img2.gif) .
. - (b)
- Find the general antiderivative of
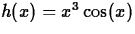 .
.
- 2.
- Let
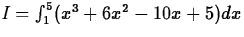
- (a)
- Approximate I by each of Tn, Sn and Mn for n = 2,4,10.
- (b)
- Use the int command to evaluate I.
- (c)
- Discuss whether the approximation methods of (a) seem to yield good approximations. Which of the three gives the best results? Why does this method give the best result for this particular problem? (Hint:Think about its error bound statement.).
- 3.
- Use Simpson's rule, the trapezoidal rule and the midpoint rule
to approximate the given integrals to four decimal places. For each
method give the number of subintervals needed and justify the number you
give. Be sure to actually give the four place approximation. Which method seems to give the best approximation?
- (a)
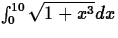
- (b)
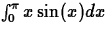
- 4.
- Use Simpson's Rule to approximate
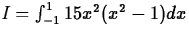 . Use
. Use 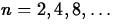 . Consider I-Sn for
. Consider I-Sn for 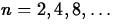 . What is the first value of n for which the error is
the maximum possible, e.g. for which the error is actually as large
as permitted by the error bound statement for Simpson's rule? Based
on your investigation, make a guess as to the value of I - Sn,
expressed as a function of n.
. What is the first value of n for which the error is
the maximum possible, e.g. for which the error is actually as large
as permitted by the error bound statement for Simpson's rule? Based
on your investigation, make a guess as to the value of I - Sn,
expressed as a function of n.



Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
Christine M Palmer
12/11/1997
![]()
![]()
![]()