$next$ $up$ $previous$
Next: About this document ... Up: Labs and Projects for Previous: Area Approximations

Exercises

1.

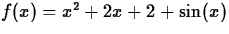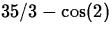Consider the function $f(x) = x^2+2x+2+\sin(x)$ on the interval [0,2]. Very soon you will be able to use calculus to determine that the area under this curve is exactly equal to $35/3-\cos(2)$ . For each of the left endpoint, right endpoint, and midpoint rules, determine the minimum number of subintervals required to approximate the area to within 0.01. Which method works best?

2.

Now consider the function 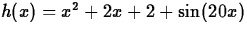$h(x)=x^2+2x+2+\sin(20x)$ on the interval [0,2]. Repeat the procedure for the previous exercise, using only the midpoint rule. That is, find the minimum number of subintervals required to approximate the area to within 0.01. (The exact value of the area in this case is 643/60 - cos(40)/20.) Explain why more subintervals are needed for this function than were required for the function in the first exercise. You might find the error bound formula helpful.

3.

Consider the function g(x) = -x⁴-2x³+3x² on the interval [-3,1].

(a): If M₃₀ is used to approximate the area under the curve, what accuracy is guaranteed by the error bound formula? Make sure you state clearly how you obtained the value of B.
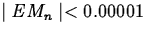(b): Use the error bound formula to find the smallest value of n that guarantees that M_n approximates the area to within 0.00001. That is, find the smallest value of n that guarantees that $\mid EM_n \mid < 0.00001$ .

4.

Consider the area under the curve 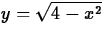$y=\sqrt{4-x^2}$ on the interval [-2,2].

(a): Use the formula for the area of a circle to compute the exact value of this area.
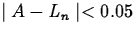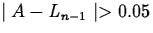(b): Using the left endpoint rule, find the minimum number of subintervals required to approximate this area to within a tolerance of 0.05. That is find the value of n such that $\mid A- L_n \mid < 0.05$ , but $\mid A- L_{n-1} \mid \gt 0.05$ .
(c): Repeat the previous part of this exercise using the midpoint rule.
(d): Explain why the error bound formula cannot be used for this function on this interval.

$next$ $up$ $previous$
Next: About this document ... Up: Labs and Projects for Previous: Area Approximations

Jane E Bouchard
11/2/1999