Exercises

1.

Consider the function f(x) = x on the interval [0,8]. Verify that the middlesum command gives the exact value for the area independent of the number of subintervals you specify. Can you explain this? Note that you can use the formula for the area of a triangle to compute that the area is 32. (Hint - look at the plot produced by the middlebox command.)

2.

Consider the function f(x) = 2x³-7x²-9 on the interval [-1,3]. Use the command leftsum to approximate the definite integral

$$\int_{-1}^{3} f(x) \, dx = - \frac{184}{3}$$

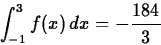
to two decimal places. Then explain why the leftsum and rightsum commands give the same numerical values for the same number of subintervals. (Hint - use the leftbox and rightbox commands to see what is going on.)

3.

Consider the function

$$g(x) = \frac{x^3+4x^2-12 x-1}{x^2+3x+5}$$

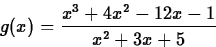
on the interval [-3,3].

(a)

If M₁₀ is used to approximate the area under the curve, what accuracy is guaranteed by the error bound formula? Make sure you state clearly how you obtained the value of B.

(b)

Use the error bound formula to find the smallest value of n that guarantees that M_n approximates the area to within 0.00001. That is, find the smallest value of n that guarantees that $\mid EM_n \mid < 0.00001$.

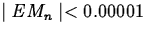4.

Suppose that g(x) is a smooth function that is strictly positive and increasing on the interval [a,b]. Is it always true that, for any n,

$$L_n \leq \int_{a}^{b} g(x) \, dx \leq R_n$$

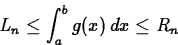
where L_n and R_n are the area approximations with n subintervals using the left endpoint rule and the right endpoint rule, respectively? Your answer should be yes. Explain why.