Subsections

• Purpose
• Background
• Exercises

Center of Mass

Purpose

The purpose of this lab is to give you practice with using integrals to determine the centroids of thin plates of uniform thickness and density, but irregular shape.

Background

In designing mechanisms or structures, one often has to deal with distributed forces, that is, forces that do not act at a discrete, finite set of points. The most common example of a distributed force is the force of gravity, which acts on all parts of any body of matter. Other examples are pressure in fluids and electrostatic forces, though there are many others.

One of the basic useful principles of analyzing distributed forces is the idea of replacing them with a single, aggregate force ${\bf F}$ that acts at a single point and is somehow equivalent to the original distributed force. This may not always be possible, but this technique has found great use in engineering and science. As a simple example, suppose we have gravity acting on a solid plate of uniform thickness and density, but irregular shape. Finding the equivalent force is really the problem of finding the point where we could exactly balance the plate. This balance point is often called the center of mass of the body.

For symmetric objects, the balance point is usually easy to find. For example, the balance point of an empty see-saw is the exact center. Similarly, the balance points for rectangles or circles are just the geometrical centers. For non-symmetric objects, the answer is not so clear, but it turns out that there is a fairly simple algorithm involving integrals for determining balance points.

We begin by restricting our attention to thin plates of. In Engineering and Science, this type of object is called a lamina. For mathematical purposes, we assume that the lamina is bounded by $x=a$, $x=b$, $y=f(x)$, and $y=g(x)$, with $g(x) \leq f(x)$. The density per unit area is given by $\delta (x)$. Then the coordinates $(\bar{x},\bar{y})$ of the center of mass are given by the following formulas.

$$\bar{x} = \frac{\int_a^b x \delta(x) (f(x)-g(x))\, dx}{\int_a^b \delta(x) (f(x)-g(x))\, dx}$$

$$\bar{y} = \frac{1}{2} \frac{\int_a^b \delta(x) (f(x)^2-g(x)^2)\, dx}{\int_a^b \delta(x) (f(x)-g(x))\, dx}$$

To see where these formulas come from, we need the following result. Suppose we have a composite body that is made up of two masses $m_1$ and $m_2$ and that we know the centers of mass are $(\bar{x}_1,\bar{y}_1)$ and $(\bar{x}_2,\bar{y}_2)$. Then according to the principles of mechanics, the center of mass of the composite body can be determined from the following equations.

$$(m_1 + m_2) \bar{x} = m_1 \bar{x}_1 + m_2 \bar{x}_2$$

$$(m_1 + m_2) \bar{y} = m_1 \bar{y}_1 + m_2 \bar{y}_2$$

This result can be easily generalized to the case where we have a composite body made up of $n$ masses to give the following result.

$$\left( \sum_{i=1}^n m_i \right) \bar{x} = \sum_{i=1}^n m_i \bar{x}_i$$

$$\left( \sum_{i=1}^n m_i \right) \bar{y} = \sum_{i=1}^n m_i \bar{y}_i$$

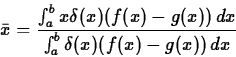
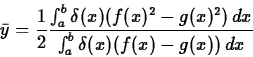
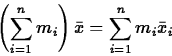
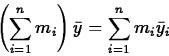
To go from these formulas to the integral formulas presented earlier, we first partition the interval $[a,b]$ into $n$ subintervals

$$a = x_0 < x_1 < \ldots < x_n = b$$

Then we approximate the lamina on each subinterval with a rectangle by letting $x_{i}^{*}$ be the midpoint of the $i\mbox{th}$ subinterval and using $f(x_{i}^{*})$ as the top of the rectangle and $g(x_{i}^{*})$ as the bottom. This gives a rectangle of width $\Delta x_i = x_i - x_{i-1}$ and height $f(x_{i}^{*}) - g(x_{i}^{*})$. Assuming that the density is 1, we have the following for the mass, $m_i$, and center of mass, $(\bar{x}_i,\bar{y}_i)$ of the $i\mbox{th}$ rectangle.

$$m_i = \delta(x_{i}^{*})(f(x_{i}^{*}) -g(x_{i}^{*})) \Delta x_i$$

$$\bar{x}_i = x_{i}^{*}$$

$$\bar{y}_i = \frac{1}{2} (f(x_{i}^{*}) +g(x_{i}^{*}))$$

Using these relations, we get the following equations.

$$\sum_{i=1}^n m_i = \sum_{i=1}^n \delta(x_{i}^{*}) (f(x_{i}^{*}) -g(x_{i}^{*})) \Delta x_i$$

$$\sum_{i=1}^n m_i\, \bar{x}_i = \sum_{i=1}^n x_{i}^* \delta(x_{i}^{*})(f(x_{i}^{*}) -g(x_{i}^{*})) \Delta x_i$$

$$\sum_{i=1}^n m_i\, \bar{y}_i = \sum_{i=1}^n \frac{1}{2} (f(x_... ...{*})) \delta(x_{i}^{*}) (f(x_{i}^{*})-g(x_{i}^{*})) \Delta x_i$$

The right hand sides of these equations should be easy to recognize as Riemann sums, so that when we take limits as $n$ goes to infinity, we get the following in our equations for the center of mass of our lamina.

$$\left(\int_a^b \delta(x) (f(x)-g(x))\, dx \right) \bar{x} = \int_a^b x \delta(x) (f(x)-g(x))\, dx$$

$$\left(\int_a^b (f(x)-g(x))\, dx \right) \bar{y} =\frac{1}{2} \int_a^b \delta(x) (f(x)^2-g(x)^2)\, dx$$

These are easy to rearrange into the equations given above.

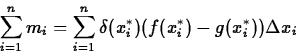
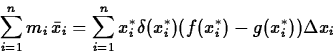
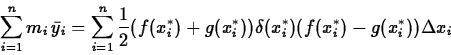
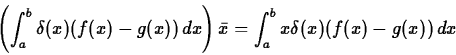
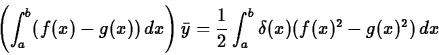
We end this section with an example, including Maple commands, for computing the center of mass. Suppose you have a lamina bounded by the curves $f(x)=x^3-3x^2-x+3$, $g(x)=3-x$, for $0 \leq x \leq 3$ and you want to compute the center of mass. To simplify things, we assume for this example that $\delta(x) =1$. To do this in Maple, we first define the two functions.

> f := x -> x^3-3*x^2-x+3;
> g := x -> 3-x;

If you are not sure about the relative positions of the two curves, it is a good idea to plot them both.

> plot({g(x),f(x)},x=0..3);

Notice that the graph of $g$ is above the graph of $f$. This means that you must switch $g$ and $f$ in the formulas.

Now we are ready to compute the center of mass. Using labels, as shown below, can help you organize your calculations and avoid mistakes. Computing the mass separately also lets you check it. If you get a negative value for the mass, something is wrong and you have to check what you have done. A common mistake is reversing the order of the functions.

> mass := int(g(x)-f(x),x=0..3);
> x_bar := int(x*(g(x)-f(x)),x=0..3)/mass;
> y_bar := 1/2*int(g(x)^2-f(x)^2,x=0..3)/mass;

As a final example, we use the same region as our previous example, but use the non-constant density $\delta(x) = 4-x/2$. The commands below show how to compute the coordinates of the center of mass. The first command defines the density. If you don't like typing out the whole word delta you can use a different letter for the density.

> delta := x -> 4-x/2; 
> mass := int(delta(x)*(g(x)-f(x)),x=0..3);
> x_bar := int(x*delta(x)*(g(x)-f(x)),x=0..3)/mass;
> y_bar := 1/2*int(delta(x)*(g(x)^2-f(x)^2),x=0..3)/mass;

Exercises

1. Find the coordinates of the center of mass of the lamina bounded by the curves $y=x^2-2$ and $y=x^2+x+4$ for $-2 \leq x \leq 3$. Assume that the density is constant. Make sure that you plot both functions on the same graph and check to see if your center of mass coordinates make sense.

2. Sometimes symmetry can help you locate the center of mass of a body. Assuming that the density is constant, use Maple to show that the center of mass of the rectangle whose vertices are the points $(-1,-1)$, $(3,-1)$, $(-1,2)$, and $(3,2)$ is the point $(1,1/2)$.

3. If the density is not constant, the symmetry of the region may not be enough to determine the center of mass. Using the same rectangle that you used in the previous example, compute the center of mass for the following densities. Explain your results. (Hint - plotting $\delta$ might help you).
   1. $\delta(x) = 1+(x^2-x)/20$
   2. $\delta(x) = 1+(x^2-2x)/2$
4. Find the coordinates of the center of mass of the lamina bounded by the curves $y=x^2$ and $y=x^2+1$ for $-3 \leq x \leq 3$. Assume the density is constant. Is the center of mass located inside the lamina or outside?