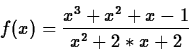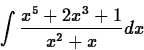Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to show how quotient functions can be integrated.
When a function is the quotient of two polynomials, you can easily take the integral if the numerator is the derivative of the denominator.
> diff(x^2+2*x+9,x);
Note that the numerator times a constant is the derivative of the denominator.
> simplify((6*x+6)/(2*x+2));
Therefore,
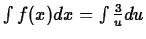 which is an easy natural log integral.
which is an easy natural log integral.
> int(3/u,u);
> subs(u=x^2+2*x+9,int(3/u,u));
To check the work, let Maple do the intgral directly.
> int((6*x+6)/(x^2+2*x+9),x);
Remember with indefinite integrals the solution adds a constant. So, the inetgral solution is
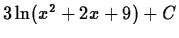 .
Often a function is not in that straight forward form. With long division, you can try and get the quotient function into the form of a polynomial plus a fraction where the numerator is a derivative of the denominator:
.
Often a function is not in that straight forward form. With long division, you can try and get the quotient function into the form of a polynomial plus a fraction where the numerator is a derivative of the denominator:
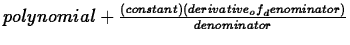 . For example if
. For example if
First execute long division and find the quotient and remainder.
> q:=quo((x^3+x^2+x-1),(x^2+2*x+2),x);
> r:=rem((x^3+x^2+x-1),(x^2+2*x+2),x);
The new form of the function is:
> f:=q+r/(x^2+2*x+2);
Note that the fractional part has the numerator a derivative times a constant 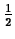 of the denominator.
of the denominator.
> diff(x^2+2*x+2,x);
> simplify*(r/diff(x^2+2*x+2,x));
> int(q,x)+subs(u=x^2+2*x+2,int(1/(2*u),u));
To check the work, let Maple do the integral directly.
> int((x^3+x^2+x-1)/(x^2+2*x+2),x);
Remember to add a constant to the indefinite integral answer:
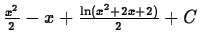 .
Show how the long division method results in the solution to the indefinite integral:
.
Show how the long division method results in the solution to the indefinite integral:
Make sure to show your steps and include plenty of text to keep your work clear. Also check your final answer by having Maple do the integral directly.
When the function is a fraction with a denominator that can be factored into linear components then the partial method can be easily used.
The denominator is easily factored:
> factor(x^2-1);
So,
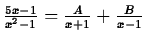 . Multiplying by the common denominator and expanding gives:
. Multiplying by the common denominator and expanding gives:
> expand(5*x-1=A*(x-1)+B*(x+1));
With this equation we can solve for 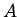 and
and 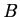 by equating the coefficients of the x term and then equating the constants. This will give us two equations which can be solved simultaneously.
by equating the coefficients of the x term and then equating the constants. This will give us two equations which can be solved simultaneously.
> solve({5*x=A*x+x*B,-1=-A+B},{A,B});
These values tell us that:
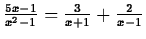 . The right-hand side shows fractions that are easily integrated with the natural log.
. The right-hand side shows fractions that are easily integrated with the natural log.
> int(3/(x+1)+2/(x-2).x);
To check the work let Maple do the integral directly.
int((5*x-1)/(x^2-1),x);
Remember the constant:
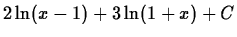 .
Use partial fractions to find the solution to the definite integral:
.
Use partial fractions to find the solution to the definite integral:
Make sure to show your steps and include plenty of text to keep your work clear. Also check your final answer by having Mapel do the integral directly.



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2006-02-13