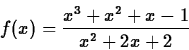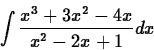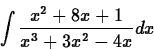Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to show how quotient functions can be integrated.
When a function is the quotient of two polynomials, you can easily take the integral if the numerator is the derivative of the denominator.
> diff(x^2+2*x+9,x);
Note that the numerator times a constant is the derivative of the denominator.
> simplify((6*x+6)/(2*x+2));
Therefore,
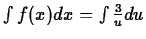 which is an easy natural log integral.
which is an easy natural log integral.
> int(3/u,u);
> subs(u=x^2+2*x+9,int(3/u,u));
To check the work, let Maple do the intgral directly.
> int((6*x+6)/(x^2+2*x+9),x);
Remember with indefinite integrals the solution adds a constant. So, the inetgral solution is
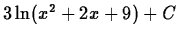 .
Often a function is not in that straight forward form. With long division, you can try and get the quotient function into the form of a polynomial plus a fraction where the numerator is a derivative of the denominator:
.
Often a function is not in that straight forward form. With long division, you can try and get the quotient function into the form of a polynomial plus a fraction where the numerator is a derivative of the denominator:
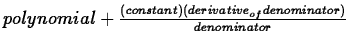 . For example if
. For example if
First execute long division and find the quotient and remainder.
> q:=quo((x^3+x^2+x-1),(x^2+2*x+2),x);
> r:=rem((x^3+x^2+x-1),(x^2+2*x+2),x);
The new form of the function is:
> f:=q+r/(x^2+2*x+2);
Note that the fractional part has the numerator a derivative times a constant 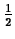 of the denominator.
of the denominator.
> diff(x^2+2*x+2,x);
> simplify(r/diff(x^2+2*x+2,x));
> int(q,x)+subs(u=x^2+2*x+2,int(1/(2*u),u));
To check the work, let Maple do the integral directly.
> int((x^3+x^2+x-1)/(x^2+2*x+2),x);
Remember to add a constant to the indefinite integral answer:
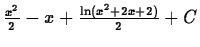 .
.
When the function is a fraction with a denominator that can be factored into linear components then the partial method can be easily used.
The denominator is easily factored:
> factor(x^2-1);
So,
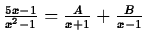 . Multiplying by the common denominator and expanding gives:
. Multiplying by the common denominator and expanding gives:
> expand(5*x-1=A*(x-1)+B*(x+1));
With this equation we can solve for 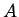 and
and 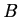 by equating the coefficients of the x term and then equating the constants. This will give us two equations which can be solved simultaneously.
by equating the coefficients of the x term and then equating the constants. This will give us two equations which can be solved simultaneously.
> solve({5*x=A*x+x*B,-1=-A+B},{A,B});
These values tell us that:
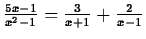 . The right-hand side shows fractions that are easily integrated with the natural log.
. The right-hand side shows fractions that are easily integrated with the natural log.
> int(3/(x+1)+2/(x-2),x);
To check the work let Maple do the integral directly.
int((5*x-1)/(x^2-1),x);
Remember the constant:
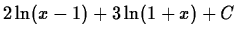 .
.
- Show how the long division method results in the solution to the indefinite integral:
Make sure to show your steps and include plenty of text to keep your work clear. Also check your final answer by having Maple do the integral directly.
- Use partial fractions to evaluate the indefinite integral:
Make sure to show your steps and include plenty of text to keep your work clear. Also check your final answer by having Mapel do the integral directly.



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2009-02-02