Background

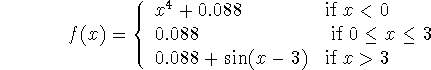
In this section, we first discuss the glass exercise from part 1 of this lab to try to clear up any confusion that may remain. Then we discuss two examples that further illustrate applications of solids of revolution.

In part 1 of this lab, one of the exercises referred to a design for a drinking glass. The idea was to come up with a function f(x) which could be revolved about the x axis over a suitable interval to produce the glass. Two students came up with the following function.

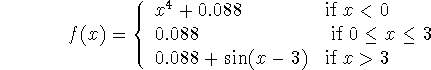
Which can be entered in Maple with the following command.

  > f := x -> if x<0 then x^4+0.088 elif x<3 then 0.088 else sin(x-3)+0.088 fi;

However, many students ran into problems with plotting this function and came up with the error shown below.

  > plot(f(x),x=-0.9..4.5);

Error, (in f) cannot evaluate boolean

The term boolean refers to the if statement in the definition of f(x) in Maple. What the error is saying is that Maple is trying to evaluate whether the statement ``if x<0'' is true or not without knowing a value of x. This cannot be done, hence the error.

The key to getting around this problem, which was shown in an example in the background section of part 1, is to use single quotes around f(x) in the plot and revolve commands, as shown below.

  > plot('f(x)',x=-0.9..4.5);

  > revolve('f(x)',x=-0.9..4.5);

Putting in the quotes tells Maple to wait until x has a numerical value before trying to evaluate f(x).

The final part of the exercise asked for the volume of the liquid-filled part of the glass. This would be

The easiest way to compute this is with the following command.

  > Pi*int((sin(x-3)+0.088)^2,x=3..4.5);

It is possible to compute this using f, as shown below, but the current release of Maple is not very smart about handling piecewise-defined functions.

  > evalf(Pi*Int('f(x)^2',x=3..4.5));

We now consider the following example. Suppose that a hole of radius 1 is to be bored through the center of a sphere of radius 2 and you are asked to compute the volume of the remaining part.

The hardest part of this example is setting it up as a solid of revolution problem. We know that we can generate a sphere of radius 2 by revolving the semi-circle about the x axis. The sphere with a hole removed from the center can be obtained by revolving the region bounded by and y=1. To see this, try the commands below.

  > g := x -> sqrt(4-x^2);

  > plot({g(x),1},x=-2..2);

To get the region right, we have to find the points where y=1 intersects the semi-circle. This is done below, and then the sphere with the hole is generated via revolve. You will probably have to move the plot around to see the hole.

  > solve(g(x)=1,x);

  > revolve({g(x),1},x=-sqrt(3)..sqrt(3));

The RevInt command can be used to set up the integral for the volume of the holed sphere in a simple way as follows.

  > RevInt({g(x),1},x=-sqrt(3)..sqrt(3));

The result of the RevInt command needs to be evaluated numerically as shown below.

  > evalf(RevInt({g(x),1},x=-sqrt(3)..sqrt(3)));

If you need an analytic answer, you are better off setting up the integral directly, as follows.

  > Pi*int(3-x^2,x=-sqrt(3)..sqrt(3));

The reason it is often better not to use RevInt is that it was designed primarily for demonstrations, and does not deal very intelligently with regions defined by two functions f and g.

As a third example, consider the following. A spherical tank of radius 25 meters is to be used to store liquid nitrogen. The tank has a sensor that reports the height of the liquid inside the tank. You have been asked to come up with a function that will convert the height of the liquid in the tank to the volume of the liquid in the tank.

We'll start by letting x be the height of the liquid in meters. Since this is a math class, it doesn't bother us at all that we'll be doing the problem with the tank on its side. First, we need a semi-circle of radius 25 and center x=25, y=0. That is we need to solve the equation

for y. If we do so, we get the equation

Revolving this curve about the x axis for gives us our tank. Now suppose we want compute the volume of liquid when the tank is filled to a height x. (Recall that we've turned the tank on its side for our calculations.) This volume can be obtained by revolving our curve from 0 to x. That is, if we set up the curve defining the boundary of our tank as follows,

  > tank := x -> sqrt(625-(x-25)^2);

then the volume is given by the following function.

  > vol := x -> Pi*int(tank(t)^2,t=0..x);

which can be plotted to give the desired curve.