


Next: About this document ...
Up: Exponentials - Part 1
Previous: Background
- 1.
- Suppose that b satisfies b > 1. Explain the relationship
between the graphs of
f(x) = bx
and
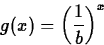
- 2.
- Suppose that f(x) is an exponential function that satisfies
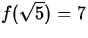 . Find the value of b so that
. Find the value of b so that
f(x) = bx
and compute the value of f(3).
- 3.
- Suppose that the population of a certain bacteria can be modeled
by an exponential function. In a particular experiment, the number of
bacteria was 50,000 at t=0. Four hours later, the number of
bacteria was 150,000. Suppose a second experiment is performed under
the same conditions, but the number of bacteria at t=0 is only
20,000. Show, using the equation for exponential growth, that the
predicted number of bacteria after four hours in this second
experiment is 60,000.
- 4.
- Suppose that for a certain drug, the following results were
obtained. Immediately after the drug was administered, the
concentration was 4.8 mg/ml. Three hours later, the concentration had
dropped to 2.23 mg/ml. Determine the value of k for this drug.
- 5.
- Suppose that for the drug in the previous exercise, the maximum
safe level is
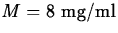 and the minimum effective level is
and the minimum effective level is
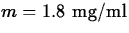 . What is the maximum possible time between doses
for this drug?
. What is the maximum possible time between doses
for this drug?



Next: About this document ...
Up: Exponentials - Part 1
Previous: Background
William W. Farr
1/23/1998
![]()
![]()
![]()
![]()