Exercises

1.

Let $f(x) = 1 + \sin(2x)/2$ and consider the interval $0 \leq x \leq \pi$. Plot the solid of revolution obtained by revolving the graph of this function around the x axis. Then compute the volume of the solid of revolution you obtained. Finally, use the LeftInt command and determine the number of subintervals needed to approximate the volume to within 0.1.

2.

Repeat the first exercise, this time using the function g(x) = 1 + x/4. The number of subintervals required should be larger than in the previous exercise. Try to explain why this happens. Some things that might help you are to compare the graphs of the two functions, to look at plots with LeftDisk, and to examine the integrals that give the volumes.

3.

Compute the volume of the solid generated by revolving the region bounded by the x-axis, the graph of the function $h(x) = (1+\sin(x)/2)\exp(-\frac{x}{5})$, x=0, and x=7.

4.

Nearly four years ago, Chris Zannella and Eric Pauly (both class of '98) were asked to design a drinking glass by revolving a suitable function about the x axis. Here is the function they came up with.

$$f(x) = \left\{ \begin{array} {ll} x^4+0.088 & \mbox{if $x <... ... \\ 0.088+\sin(x-3) & \mbox{if $x \gt 3$} \end{array}\right.$$

They obtained the shape of their glass by revolving this function about the x axis over the interval [-0.9,4.5]. The Maple command they used to define this function is given below.

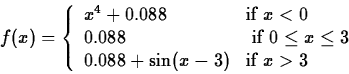
  > pz := x -> piecewise(x<0,x^4+0.088,x <=3,0.088,0.088+sin(x-3));

Plot this function (without revolving it) over the interval [-0.9,4.5] and identify the formula for each part of the graph. Then, revolve this function about the x axis over the same interval and comment on the glass Eric and Chris designed. Finally, compute the volume of the part of this glass that could be filled with liquid, assuming the stem is solid. (Hint - your integral will involve only one of the formulas used to define the function.)