


Next: About this document ...
Up: Labs and Projects for
Previous: Area Approximations
- 1.
- Consider the function f(x) = 4-x on the interval [0,4]. Verify
that the middlesum command gives the exact value for the area
independent of the number of subintervals you specify. Can you explain
this? Note that you
can use the formula for the area of a triangle to compute that the
area is 8. (Hint - look at the plot produced by the middlebox
command.)
- 2.
- Consider the general linear function g(x) = cx+d, where c
and d are constants. What does the error bound formula say about the
accuracy of the midpoint rule for approximating
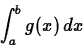
Does this make sense, based on your result for the first exercise?
Explain.
- 3.
- Consider the function f(x) = x4-5x3+12x2-x+1 on the interval
[0,5]. Use the command leftsum to
approximate the definite integral
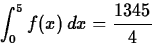
to two decimal places. Looking at the graph of f, can you explain
why value given by the leftsum command is always less than
the value of the integral? If you used the rightsum command,
to approximate this same integral, do you think your approximations
would be smaller than the value of the integral, larger than the
integral, or could it be larger or smaller depending on the number of
subintervals you use? Explain your answer.
- 4.
- Consider the function
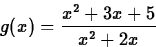
on the interval [1,8].
- (a)
- Use the error bound formula to find the smallest value of n that
guarantees that Mn approximates the area to within 0.001. That
is, find the smallest value of n that guarantees that
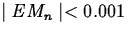 .
.
- (b)
- The value of n given by the error bound is usually
conservative. That is, in practice the desired accuracy can be
achieved with a smaller value of n. Given that
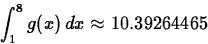
find the smallest value of n such that 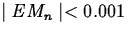 .
.



Next: About this document ...
Up: Labs and Projects for
Previous: Area Approximations
Jane E Bouchard
3/24/2000
![]()
![]()
![]()
![]()
![]()
![]()
![]()