- As explained in your text, the position of the object at
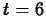 is equal to the area under the velocity curve from
is equal to the area under the velocity curve from 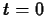 to
to 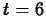 . Use
the midpoint rule with
. Use
the midpoint rule with 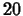 subdivision to approximate the position of
the object at
subdivision to approximate the position of
the object at 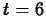 .
.
- Let
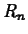 be the right endpoint rule and
be the right endpoint rule and 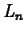 the left endpoint
rule approximations with
the left endpoint
rule approximations with 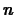 subdivisions to the position of the
object at
subdivisions to the position of the
object at 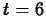 . Explain why the following relation holds for any
value of
. Explain why the following relation holds for any
value of 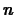 .
.
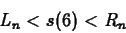
(Hint - look at the results of leftbox and rightbox commands.) - Evaluate
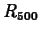 and
and 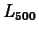 . Based on your results, do
you think your approximation using the midpoint rule with
. Based on your results, do
you think your approximation using the midpoint rule with 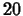 subintervals was within
subintervals was within 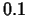 of the exact value for the area? Explain
why or why not.
of the exact value for the area? Explain
why or why not.
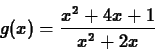
on the interval
- Use the error bound formula to find the smallest value of
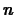 that
guarantees that
that
guarantees that 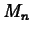 approximates the area to within
approximates the area to within 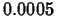 . That
is, find the smallest value of
. That
is, find the smallest value of 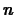 that guarantees that
that guarantees that
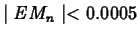 .
.
- The value of
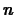 given by the error bound is usually
conservative. That is, in practice the desired accuracy can be
achieved with a smaller value of
given by the error bound is usually
conservative. That is, in practice the desired accuracy can be
achieved with a smaller value of 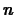 . Given that
. Given that
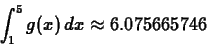
find the smallest value of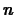 such that
such that
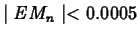 .
.