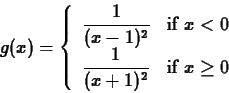Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
Subsections
The purpose of this lab is to introduce you to the definite integral
and to Maple commands for computing definite integrals.
There are two main ways to think of the definite integral. The easiest
one to understand, and the one we'll consider first, is as a means for
computing areas (and volumes). The second way the definite integral is
used is as a sum. That is, we use the definite integral to ``add
things up''. Here are some examples.
- Computing net or total distance traveled by a moving object.
- Computing average values, e.g. centroids and centers of mass,
moments of inertia, and averages of probability distributions.
Of course, when we use a definite integral to compute an area or a
volume, we are adding up area or volume. So you might ask why make a
distinction? The answer is that the notion of an integral as a means
of computing an area or volume is much more concrete and is easier to
understand.
You have learned in class that the definite integral is actually defined
as a (complicated) limit of sums, so it makes sense that the integral
should be thought of as a sum. You have also learned in class that the
indefinite integral, or anti-derivative, can be used to evaluate
definite integrals. Students often concentrate
on techniques for evaluating integrals, and ignore the
definition of the integral as a limit of sums. This is a mistake, for the
following reasons.
- Many functions don't have anti-deriviatives that can be written
down as formulas. Definite integrals of such function must be done
using numerical techniques, which always depend on the definition of
the integral as a limit of sums.
- In many applications of the integral in engineering and science,
you aren't given the function which is to be integrated and must
derive it. The derivation always depends on the notion of the
integral as a sum. You will see examples of this later on in the course.
The basic Maple command for computing definite and indefinite
integrals is the int command. The syntax is very similar to
that of the leftsum and rightsum commands, except
you don't need to specify the number of subintervals.
Suppose you wanted to compute the following definite
integral with Maple.
The command to use is shown below.
>
int(x^2,x=0..4);
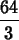
Notice that Maple gives an exact answer, as a fraction. If you want a
decimal approximation to an integral, you just put an evalf
command around the int command, as shown below.
>
evalf(int(x^2,x=0..4));
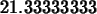
To compute an indefinite integral with Maple, you just leave out the
range for the limits of integration, as shown below.
>
int(x^2,x);
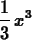
Note that Maple does not include a constant of integration.
You can also use the Maple int command with functions or
expressions you have defined in Maple.
For
example, suppose you wanted to find area under the curve of the
function
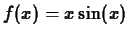 on the
interval
on the
interval ![$[0,\pi]$](img6.gif) . Then you can define this function in Maple with
the command
. Then you can define this function in Maple with
the command
>
f := x -> x*sin(x);
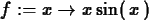
and then use this definition as shown below.
>
int(f(x),x=0..Pi);
You can also simply give the expression corresponding to 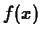 a
label in Maple, and then use that label in subsequent commands as
shown below. However, notice the difference between the two
methods. You are urged you to choose one or the other, so you don't
mix the syntax up.
a
label in Maple, and then use that label in subsequent commands as
shown below. However, notice the difference between the two
methods. You are urged you to choose one or the other, so you don't
mix the syntax up.
>
p := x*sin(x);
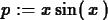
>
int(p,x=0..Pi);
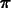
The same int command works to compute any
definite integral, whether it corresponds to an area or not. For
example, to compute the definite integral
you could use the following Maple command.
>
int((2*x-3)^5,x=-2..4);
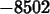
Sometimes you need to compute a definite integral involving a
piecewise-defined function. For example, suppose you have a function
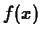 defined as follows
defined as follows
and you needed to compute the definite integral
The best way to do this in Maple is to split it up into two integrals
and use the appropriate formula, as shown below. How you split the
integral up is determined by where the formula defining the function
changes.
>
int(2-x^2,x=-5..1)+int(x,x=1..5);
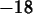
If a function 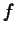 is integrable over an interval
is integrable over an interval ![$[a,b]$](img17.gif) , then we
define the average value of
, then we
define the average value of 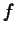 , which we'll denote as
, which we'll denote as 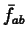 ,
on this interval to be
,
on this interval to be
Note that the average value is just a number. Note furthermore that we
can rearrange the definition to give
If 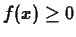 on
on ![$[a,b]$](img17.gif) , then the average value has the following
geometrical interpretation:
, then the average value has the following
geometrical interpretation: 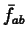 is the height of a
rectangle of width
is the height of a
rectangle of width 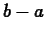 such that the area of this rectangle is equal
to the area under the graph of
such that the area of this rectangle is equal
to the area under the graph of 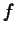 from
from 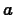 to
to 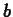 . The following
example shows you how to compute an average. The last plot command
shows the function and the top of this rectangle.
. The following
example shows you how to compute an average. The last plot command
shows the function and the top of this rectangle.
>
f :=x -> x*sin(x) ;
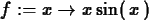
>
plot(f(x),x=0..Pi);
>
f_ave := int(f(x),x=0..Pi)/Pi;
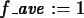
>
plot(f(x),f_ave,x=0..Pi);
- For each of the following functions and intervals, determine the
area under the curve using the Maple int command. Include a
plot of the curve to verify that it is non-negative over the interval
in question.
-
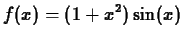 on
on ![$[0,\pi]$](img6.gif) .
.
-
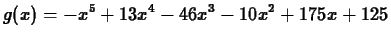 on
on
![$[-1,4]$](img28.gif) .
.
-
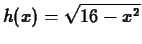 on
on ![$[0,4]$](img30.gif) . Verify that the
answer you get is correct by using the formula for the area of a circle.
. Verify that the
answer you get is correct by using the formula for the area of a circle.
- Suppose that the flow rate of water, in units of 1000 cubic feet per
hour, over the spillway of a dam
is given by
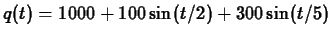 where
where 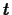 is time in hours. The total flow,
is time in hours. The total flow, 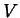 , over the
spillway from time
, over the
spillway from time 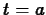 to
to 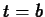 is given by
is given by
where the units of 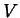 are thousands of cubic feet.
are thousands of cubic feet.
- Compute the total flow over the spillway for the interval
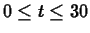 , where
, where 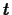 is the time in hours.
is the time in hours.
- Compute the average flow rate of water, in units of 1000 cubic
feet per hour, over the spillway for the
time period
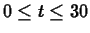 .
.
- Consider the function
Compute the following integral.



Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
William W. Farr
2001-03-26
![]() on the
interval
on the
interval ![]() . Then you can define this function in Maple with
the command
. Then you can define this function in Maple with
the command
![]() a
label in Maple, and then use that label in subsequent commands as
shown below. However, notice the difference between the two
methods. You are urged you to choose one or the other, so you don't
mix the syntax up.
a
label in Maple, and then use that label in subsequent commands as
shown below. However, notice the difference between the two
methods. You are urged you to choose one or the other, so you don't
mix the syntax up.
![]() defined as follows
defined as follows
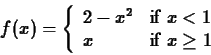
![]() on
on ![]() , then the average value has the following
geometrical interpretation:
, then the average value has the following
geometrical interpretation: ![]() is the height of a
rectangle of width
is the height of a
rectangle of width ![]() such that the area of this rectangle is equal
to the area under the graph of
such that the area of this rectangle is equal
to the area under the graph of ![]() from
from ![]() to
to ![]() . The following
example shows you how to compute an average. The last plot command
shows the function and the top of this rectangle.
. The following
example shows you how to compute an average. The last plot command
shows the function and the top of this rectangle.