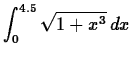Subsections

• Purpose
• Background
  • Introduction
  • Definite and indefinite integrals with Maple
  
  
• Exercises

The Definite Integral

Purpose

The purpose of this lab is to introduce you to Maple commands for computing definite and indefinite integrals.

Background

Introduction

There are two main ways to think of the definite integral. The easiest one to understand is as a means for computing areas (and volumes). The second way the definite integral is used is as a sum. That is, we use the definite integral to ``add things up''. Here are some examples.

• Computing net or total distance traveled by a moving object.
• Computing average values, e.g. centroids and centers of mass, moments of inertia, and averages of probability distributions.

This lab is intended to introuduce you to Maple commands for computing integrals, including applications of integrals.

Definite and indefinite integrals with Maple

The basic Maple command for computing definite and indefinite integrals is the int command. The syntax is very similar to that of the leftsum and rightsum commands, except you don't need to specify the number of subintervals. Suppose you wanted to compute the following definite integral with Maple.

$$\int_{0}^{4} x^2 dx$$

The command to use is shown below.

> int(x^2,x=0..4);

Notice that Maple gives an exact answer, as a fraction. If you want a decimal approximation to an integral, you just put an evalf command around the int command, as shown below.

> evalf(int(x^2,x=0..4));

To compute an indefinite integral with Maple, you just leave out the range for the limits of integration, as shown below.

> int(x^2,x);

Note that Maple does not include a constant of integration.

You can also use the Maple int command with functions or expressions you have defined in Maple. For example, suppose you wanted to find area under the curve of the function $f(x)=x \sin(x)$ on the interval $[0,\pi]$. Then you can define this function in Maple with the command

> f := x -> x*sin(x);

and then use this definition as shown below.

> int(f(x),x=0..Pi);

You can also simply give the expression corresponding to $f(x)$ a label in Maple, and then use that label in subsequent commands as shown below. However, notice the difference between the two methods. You are urged to choose one or the other, so you don't mix the syntax up.

> p := x*sin(x);
> int(p,x=0..Pi);

If you want to find the area bounded by the graph of two functions, you should first plot both functions on the same graph. You can then find the intersection points using either the solve or fsolve command. Once this is done, you can calculate the definite integral in Maple. An example below illustrates how this can be done in Maple by finding the area bounded by the graphs of $f(x)=-x^2+4x+6$ and $g(x)=x/3+2$:

> f := x-> -x^2+4*x+6; 
> g := x-> x/3+2;
> plot({f(x),g(x)},x=-2..6);
> a := fsolve(f(x)=g(x),x=-2..0);
> b := fsolve(f(x)=g(x),x=4..6);
> int(f(x)-g(x),x=a..b);

Exercises

1. Use Maple to compute the following definite integrals.

   A

   $$\int_{0}^{4.5} \sqrt{1+x^3} dx$$

   B

   $$\int_{-2}^{-1.5} \frac{(2x-7)^3}{3x^5+3x^3+4} dx$$

2. Use the function of a semi-circle of radius one to show that the area of a circle is $\pi$.
3. Find the area of the region bounded by the curves $$f(x)=\sqrt{x^2-x+1}$$ and $$g(x)=\cos(x)+\sin(x)$$. Include a plot of the region.

4. Find the area of the region bounded by the curves $y=x^2+1$, $y=-2x$ and $y=2x$. Include a plot of the region. (Hint: You may need to evaluate two integrals.)